Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.2 - Ex. 29
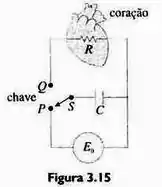
Um marcapasso, como mostrado na Figura 3.15, consiste em uma bateria, um capacitor e o coração como resistor. Quando a chave está em , o capacitor é carregado; quando está em , o capacitor é descarregado, enviando um impulso elétrico ao coração. Durante esse tempo, a voltagem aplicada ao coração é dada por:
Em que e são constantes. Determine se . (É claro que a chave é aberta e fechada periodicamente para simular o batimento cardíaco natural.)
Passo 1
A equação que nos foi dada é:
O que precisamos fazer é apenas resolver essa expressão! Para facilitar nossa visualização vamos voltar para as variáveis que estamos acostumados? Vamos chamar:
E então teremos:
E essa equação dá pra resolver por variáveis separáveis, saca só:
Integrando ambos os lados:
Então bora que bora resolver isso aí!
Passo 2
Para a primeira integral, teremos:
Que é o resultado mais conhecido do muuundo! Para a segunda integral:
Logo:
Unindo as constantes:
Simplificando:
Voltando para e , teremos:
Show! Encontramos nossa expressão!
Passo 3
O enunciado nos dá a condição inicial . Aplicando o ponto, teremos:
Substituindo na nossa solução, teremos:
Simplificando:
E essa é a nossa expressão, galera! 😊