Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.7 - Ex. 9
Uma massa de 20g estica uma mola de . Suponha qye a massa também está presa a um amortecedor viscoso com uma constante de amortecimento de . Se a massa for puxada para baixo mais e depois for solta, encontre sua posição em qualquer instante . Faça o gráfico de em função de . Determine a quase frequência e o quase período . Determine a razão entre o quase período e o período do movimento correspondente sem amortecimento. Encontre, também, o instante tal que para todo .
Passo 1
Da Eq.(21) temos que vibrações livres amortecidas são dada por
Onde é a massa, está relacionado com a resistência e a constante do material.
Assim como já resolvemos outras vezes, tome como solução tendo como solução característica
Com
Passo 2
Vamos lá
Com as informações dada, temos que
Assim
É nossa equação diferencial
Arrumando
O que torna um pouco mais fácil de resolver nosso problema.
Se tomarmos como solução temos como equação característica
Com solução
Onde teremos
Que podemos escrever como
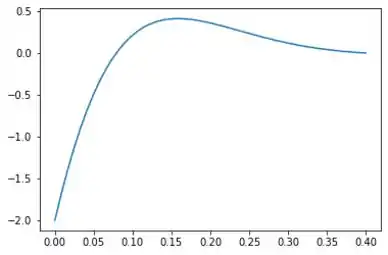
Passo 3
Agora vamos olhar prara nossas conuções iniciais. e
Assim temos
O que nos da
Assim temos então
Agora olhando para nossa solução, temos que a frequência é definida como
E o período
Passo 4
Se não houvesse amortecimento, então teríamos
Que resolvendo teríamos e
Assim a ração entre o período com amortecimento e sem é
Usando um software computacional, temos que implica em um