Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 34
34. A medida de um ângulo agudo de um triângulo retângulo está decrescendo a uma taxa de rad/s. Se o comprimento da hipotenusa for constante e igual a 40cm, ache a velocidade com que a área está variando, quando a medida do ângulo agudo for
Passo 1
Vamos seguir os seguintes passos para resolver qualquer questão de taxas:
- Leia cuidadosamente o problema.
- Se possível, faça um diagrama.
- Indentificar as variáveis e as constantes do problema.
- Escreva uma equação que relacione as variáveis.
- Derive em ambos os lados em relação a t usando regra da cadeia.
- Substituir o que foi dado e encontrar o que foi pedido.
Se liga no triângulo da questão:
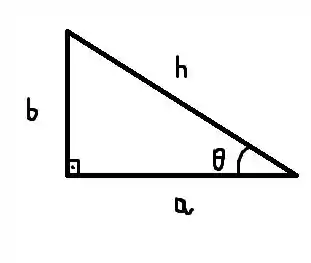
Não ajudou muito né, mas calma aí que você vai sair daqui aprendendo a fazer essa questão de olho fechado.
Vamos anotar as variáveis desse problema:
h o comprimento da hipotenusa é constante.
ângulo formado por h e a.
A área do triângulo.
A questão nos deu:
E nos pede para entramos a taxa de variação da área, , quando o ângulo for .
Passo 2
Precisamos de uma fórmula que relacione área, com a hipotenusa e o ângulo do triângulo, você conhece uma assim ? -irineu, você não sabe nem eu hsuaohsouah.
Mas sabemos que a área de um triângulo é dado por:
E podemos usar nosso conhecimentos de trigonometria para aparecer algum ângulo nessa fórmula, veja só:
Substituindo o que encontramos na fórmula da área:
Pronto, já temos uma fórmula relacionando área, ângulo e a hipotenusa.
Passo 3
Já ilustramos o que a questão pediu, já encontramos a equação que descreve o problema, agora só falta derivar.
Derivando em ambos os lados em relação a t:
Lembrando que é constante, então
Usando regra do produto para derivar: