Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 54
Para medir a temperatura são usados graus Celsius ou graus Fahrenheit . Ambos os valores de e representam a temperatura em que a água congela e ambos os valores e representam a temperatura de fervura da água. Suponha que a relação entre as temperaturas expressas nas duas escalas pode ser representada por uma reta.
a) Determine a função do primeiro grau que dá a temperatura em , quando ela é conhecida em .
b) Esboce o gráfico de .
c) Qual a temperatura em corresponde a ?
d) Existe alguma temperatura que tem o mesmo valor numérico em e em ?
Passo 1
a) Então pessoal, o enunciado pede para que encontremos uma função do tipo , no qual faz o papel de variável independente. Bom, o que temos de informação é que a função é de primeiro grau, então deve ter o seguinte formato:
No qual e são constantes. O que precisamos determinar é exatamente essas constantes e para isso vamos utilizar os dados que a questão nos fornece! Temos que:
Isso nos dá um sisteminha para resolver, não é mesmo? Então bora lá!
Passo 2
Se montarmos o sisteminha, teremos o seguinte:
Da primeira equação podemos tirar que , certo? Substituindo na segunda equação, teremos:
Sendo assim, nossa função será a seguinte:
Que é a equação de primeiro grau que queríamos encontrar!
Passo 3
b) Utilizando uma calculadora gráfica para plotar o gráfico ou dando valores para , obteremos o seguinte, galera:
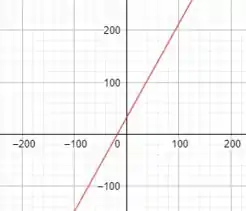
No qual os pontos realmente coincidem com o que o enunciado nos informa! 😉
Passo 4
c) Para resolvermos essa questão basta utilizarmos a expressão que encontramos no passo , que é:
Para , temos que vale:
Passo 5
d) Para descobrirmos basta igualarmos a função com , se liga:
Resposta
a)
b)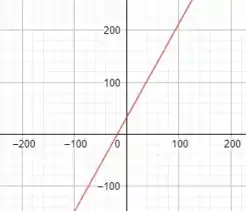 
c)
d)