O método esboçado no Problema 30 pode ser usado em qualquer equação homogênea. Ou seja,

a substituição y = xυ(x) transforma uma equação homogênea em uma equação separável. Esta

última equação pode ser resolvida por integração direta, e depois a substituição de υ por y/x

fornece a solução da equação original. Em cada um dos problemas de 31 a 38:

(a) Mostre que a equação dada é homogênea.

(b) Resolva a equação diferencial.

(c) Desenhe um campo de direções e algumas curvas integrais. Elas são simétricas em relação

à origem?

(b) Antes de determinar o comportamento da solução, precisamos encontrar qual é a solução final da EDO acima, é visto que ela é do tipo que pode separar para calcular a solução. A resolução dela é bem parecida com o que fizemos anteriormente em EDO de primeira ordem. Vamos fazera substituiçãode .

Assim, temos:

(b) Quando olhamos a equação, percebemos que agora ela é uma EDO do tipo separável.

Agora para termos uma equação dependendo de y e de v, basta integrar dos dois lados

Integrando dos dois lados, temos:

Só que no ínicio consideramos que

Ou seja, temos que:

C) As curvas abaixo foram construídas quando obteve tais valores:

Reta verde –

Reta azul –

Reta cinza –

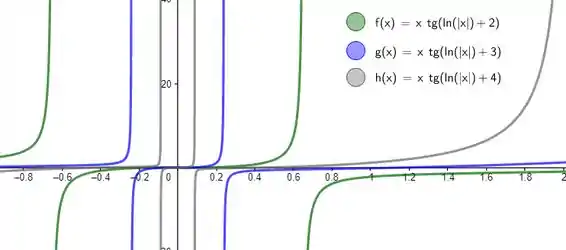
São simétricas em relação a origem.