Um modelo para a concentração no instante de uma droga injetada na corrente sanguínea é
Onde são constantes positivas e . Esboce o gráfico da função concentração. O que o gráfico nos diz sobre como a concentração varia conforme o tempo passa?
Passo 1
Eaeee, belezinha?
Bom, essa questão quer que esbocemos o gráfico da função concentração no instante de uma droga injetada na corrente sanguínea.
Para isso, o enunciado nos dá a seguinte expressão:
Onde são constantes positivas e .
Para podermos esboçar o gráfico, temos que ter alguma ideia sobre domínio, interceptações nos eixos e pontos de máximo e mínimo.
E aí?? Bora lá?? 😉
Passo 2
Perceba que o domínio da função são todos os reais positivos (o tempo é sempre positivo) e que o gráfico intercepta o eixo e o quando .
Além disso, sendo
calculando a primeira derivada obtemos pela regra da cadeia:
E lembrando que se a derivada for igual a zero, temos um ponto crítico que pode ser o valor máximo ou mínimo da função. Lembrando que

Então, fazendo
E isolando o , temos:
e
Que são nossos pontos críticos.
Também olhando para o sinal da derivada, podemos concluir que:
E, é crescente em
e decrescente em
o que torna o nosso primeiro ponto crítico um máximo local.
Passo 3
Também podemos estudar a concavidade da função, usando a segunda derivada, pois se:
![]()
Então vem ver tudo isso. Derivando novamente a função, vamos obter:
E vemos que sempre teremos:
O que nos remete a uma concavidade voltada para baixo.
Passo 4
Agora, juntando todas as informações que temos, vamos esboçar o gráfico da função.
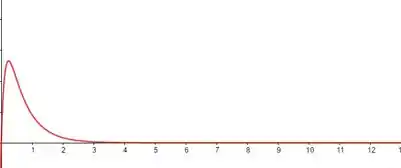
Observando o gráfico, temos que a concentração tem um ápice, ou seja, um ponto de máximo, e em seguida começa a diminuir à medida que o tempo passa, chegando a tender a zero.
Entendeu direitinho?? Responde aee😉
Resposta
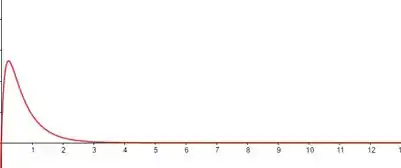
À medida que o tempo passa, a concentração tende a zero.