Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.4 - Ex. 23
Em um modelo de crescimento sazonal, uma função periódica do tempo é introduzida para considerar variações sazonais na taxa de crescimento. Essas variações podem, por exemplo, ser causadas por mudanças sazonais na oferta de alimentos.
(a) Encontre a solução do modelo de crescimento sazonal
onde e são constantes positivas.
(b) Traçando a solução para vários valores de e , explique como os valores de e afetam a solução. O que você pode dizer sobre ?
Passo 1
(a) Beleza, pessoal? Vamos resolver a equação diferencial do modelo de crescimento sazonal:
Ela é separável, né? Então agora é só integrar cada lado:
Passo 2
Pra resolver a integral da direita, use a substituição , beleza?
Agora vamos descobrir a constante usando , ok?
Temos então:
Passo 3
(b) Agora vamos traçar a solução para vários valores de e beleza?
Aqui vemos que se aumenta, então a amplitude do gráfico aumenta
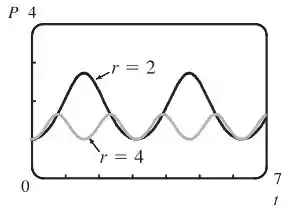
Mas se aumenta, tanto a amplitude como o período do gráfico diminuem
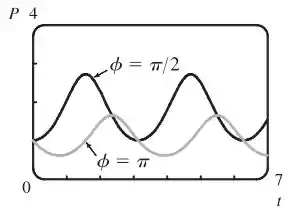
Uma mudança em produz ligeiros deslocamentos na fase e na amplitude do gráfico
Passo 4
Show! Vamos tentar calcular o limite:
Mas lá no Cálculo a gente viu que o limite de não existe, né?
Então esse limite não existe! E até faz sentido porque quando fizemos os gráficos, vimos que a função sempre está oscilando.
Resposta
(a)
(b) não existe