Um modelo de foguete é lançado para cima a partir do repouso. Sua aceleração para os três primeiros segundos é , e nesse ínterim o combustível acaba, e ele se transforma em um corpo em queda livre. Após 17 s o para-quedas do foguete se abre, e a velocidade (para baixo) diminui linearmente para -18 pés/s em 5 segundos. O foguete então cai até o solo naquela taxa.
b) Em que instante o foguete atingiu sua altura máxima e qual é essa altura.
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão fala pra gente que um modelo de foguete é lançado para cima a partir do repouso.
Sua aceleração para os três primeiros segundos é
e nesse ínterim o combustível acaba, e ele se transforma em um corpo em queda livre.
Após 17 s o para-quedas do foguete se abre, e a velocidade (para baixo) diminui linearmente para -18 pés/s em 5 segundos.
O foguete então cai até o solo naquela taxa.
Teremos que descobrir em que instante o foguete atingiu sua altura máxima e qual é essa altura.
Para isso, precisaremos lembrar que na altura máxima o foguete para, e sua velocidade vai a zero. Depois o foguete inverte seu movimente e começa a cair em direção ao solo.
Assim, vamos atrás de sua função da velocidade e da altura usando os conceitos de antuderivada.
Vem que te mostro tudinho no passo a passo.
Passo 2
Pelo esboço do gráfico no item (a) podemos ver que a altura máxima ocorre no intervalo ,
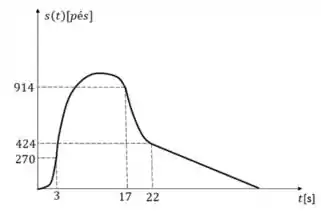
quando a velocidade é dada por:
A altura máxima ocorre quando a velocidade é zero, então:
Passo 3
Calculamos então a altura máxima através da função de para esse intervalo: