Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.10 - Ex. 78a
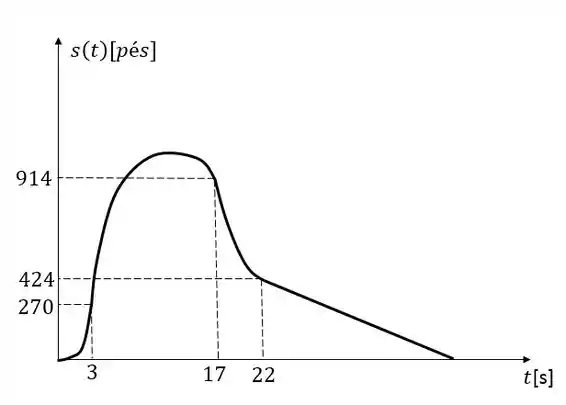
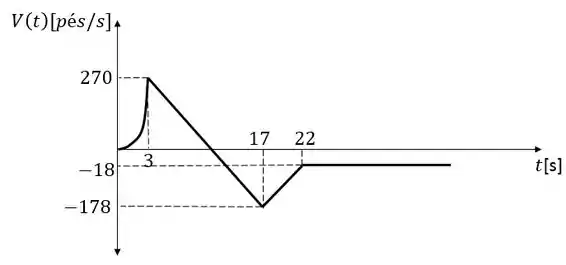
Um modelo de foguete é lançado para cima a partir do repouso. Sua aceleração para os três primeiros segundos é , e nesse ínterim o combustível acaba, e ele se transforma em um corpo em queda livre. Após 17 s o para-quedas do foguete se abre, e a velocidade (para baixo) diminui linearmente para em 5 segundos. O foguete então cai até o solo naquela taxa.
- Determine a função posição e a função velocidade (para todo instante ). Esboce os gráficos de e .
Passo 1
Queridos amigos da rede!
Temos nessa questão um foguete que parte do repouso
E que possui uma aceleração para cima igual a durante os primeiros três segundos.
Depois até o segundo , o foguete cai em queda livre, ou seja, sua aceleração é a aceleração da gravidade para baixo.
Então o paraquedas do foguete se abre e sua velocidade diminui para em de forma linear. Não sabemos o valor da aceleração aqui, mas como a velocidade diminui linearmente, podemos calcula-la fazendo:
Sendo que , logo:
Então o foguete cai até o solo com essa velocidade final.
Para cada intervalo de tempo com aceleração distinta mencionado, vamos achar as funções da posição e da velocidade . Se temos a função da aceleração, encontramos a velocidade através da antiderivada. Com a função da velocidade, aplicamos a antiderivada novamente para encontrar a função da posição.
A antiderivada é uma função que quando derivamos resulta em :
E se é uma antiderivada de nesse intervalo, então a antiderivada mais geral de é:
onde é uma constante qualquer, afinal, quando derivamos a constante obtemos zero, logo somar uma constante a não muda em nada sua derivada.
Aqui vamos usar as seguintes regras de antiderivada com relação a variável .
A antiderivada da constante:
E a antiderivada do polinômio:
Passo 2
Primeiro, para , temos uma aceleração dada por:
Achamos através da antiderivada:
Logo, somando a constante ,
Como a velocidade inicial é zero:
Agora fazemos a antiderivada novamente, para encontrar a posição:
Logo somando a constante temos:
Como a posição inicial é zero:
Passo 3
Agora, para , temos uma queda livre. A aceleração é então a aceleração da gravidade. Seu valor é negativo pois colocamos o referencial positivo para cima:
Aplicando a antiderivada chegamos à velocidade:
Logo, somando a constante temos:
A velocidade para é dada pela função encontrada no Passo 2:
Agora igualandoa velocidade em encontrada através da expressão do Passo 2 com a velocidade em encontrada através da expressão aqui do Passo 3, temos:
Portanto,
Então achamos para esse intervalo:
Somando a constante temos:
A posição para é dada pela função do passo anterior:
Então encontramos :
Portanto,
Passo 4
Agora, para o terceiro intervalo, a velocidade decresce linearmente até , de a . A aceleração é a taxa de variação da velocidade, e pode ser calculada por:
O valor de é encontrado na função de para :
Então:
Logo, a velocidade no trecho , pode ser dada por:
Como , temos:
Portanto,
Aplicando a antiderivada para chegar à função da posição:
Somando a constante temos:
O valor de é encontrado na expressão de para :
Agora aplicamos na expressão de para para encontrar :
Portanto,
Passo 5
Para o último intervalo, temos a velocidade constante, igual -18 pés/s:
Então a posição é dada por:
Somando uma constante temos:
A posição para é dada pela expressão do intervalo anterior:
Então:
Passo 6
As funções completas de posição e velocidade são então dadas por:
Com isso podemos esboçar as funções:
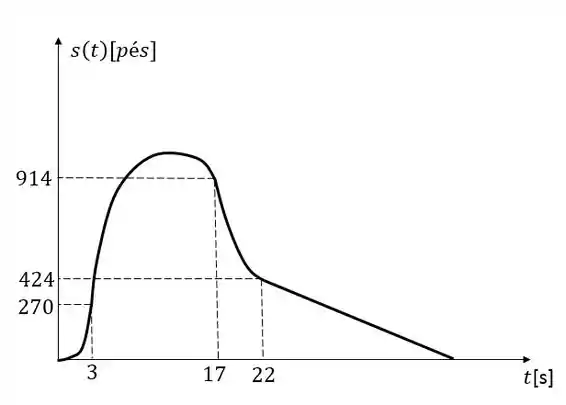
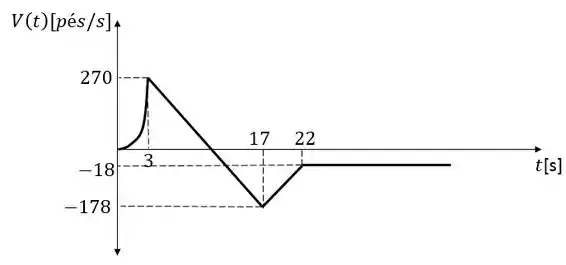
Resposta
