Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 67
Mostrar que o paralelepípedo retângulo de maior volume que pode ser colocado dentro de uma esfera tem a forma de um cubo.
Passo 1
Beleza galera, vamos olhar o nosso paralelepípedo retângulo mais de perto:
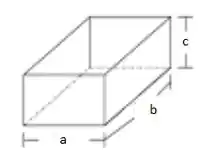
Para que ele tenha a forma de cubo, acharemos que , certo?
Para que este paralelepípedo caiba na nossa esfera de raio r, o que deverá acontecer?
Acertou quem disse que a diagonal dele deverá ter o valor do diâmetro da esfera, vamos olhar desenho:
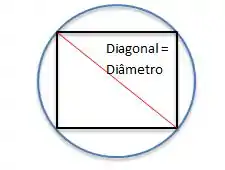
A diagonal é dada por:
E o diâmetro:
Neste caso nós temos um problema de otimização restrita, ou seja, queremos encontrar o valor máximo para o volume, mas sabendo que
Elevando ambos os lados ao quadrado:
Então, nós teremos o seguinte problema de otimização:
Passo 2
Colocando na fórmula de Lagrange:
Derivando L em relação às variáveis a, b e c e igualando as derivadas a zero:
Igualando as duas primeiras equações nós achamos:
Se igualamos a segunda e a terceira achamos:
Como estamos nos tratando de medidas, teremos o valor positivo.
Ou seja:
E já sabemos que representa um cubo, não é?!
E fim galerinhaa!
Resposta