Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.10 - Ex. 28

Mostrar que as regiões R_1 e R_2 , têm a mesma área

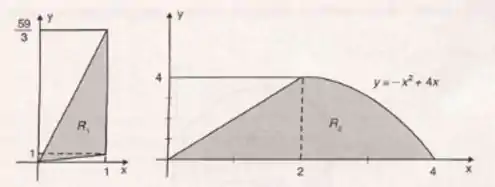
Passo 1

Como o exercício se trata do cálculo de áreas a primeira coisa que deve nos vir a cabeça é a palavra integral. Pois a integral é a área com sinal.

Lembra como é o cálculo da área entre duas funções ??

Se f (x) >= g (x) para vvv x in [a , b] então A ( á r e a e n t r e o s g r á f i c o s ) é calculada por:

A = int_a^b (f (x) - g (x)) d x

Passo 2

Cálculo de R_1 :

Seja

f (x) = (59)/(3) x e g (x) = x

R_1 = int_0^1 ((59)/(3) x - x) d x = int_0^1 ((59)/(3) x - (3)/(3) x) d x = int_0^1 ((5 6)/(3) x) d x = (28)/(3) x^2 (​|_0 -> 1 = (28)/(3)

Cálculo de R_2 :

Seja

f (x) = - x^2 + 4 x e g (x) = 0

R_2 = int_2^4 (- x^2 + 4 x - 0) d x = int_2^4 (- x^2 + 4 x) d x = - (x^3)/(3) + 2 x^2 (​|_2 -> 4 = (16)/(3)

O cálculo da área para x entre 2 e 4 basta calcularmos a área do triangulo retângulo que é definido por:

S = (1)/(2) (p r o d u t o d o s c a t e t o s)

S = (1)/(2) (4 xx 2) = 4

R_2 = (16)/(3) + (1 2)/(3) = (28)/(3)

Resposta

R_2 = (16)/(3) + (12)/(3) = (28)/(3)

R_1 = (28)/(3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule
Calcule
Calcule
Calcule
Calcule