Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 22
Tente estimar as coordenadas do ponto máximo e do ponto extremo esquerdo na curva , . Então encontre as coordenadas exatas. Quais são as assíntotas dessa curva?
Passo 1
O problema fornece a equação paramétrica de uma curva:
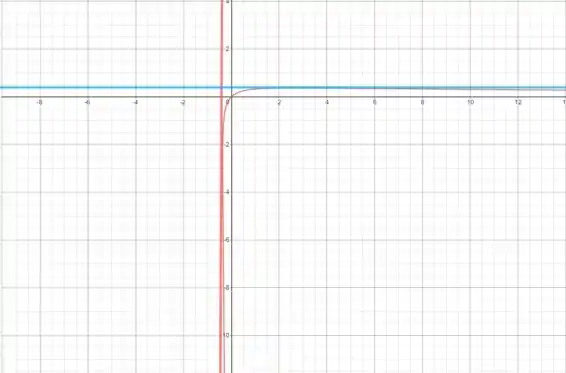
Para estimar o ponto máximo e o ponto extremo esquerdo da curva, vamos fazer um esboço. Usando o DESMOS (você pode usar o programa que quiser), obtive o seguinte:
Se você tiver curiosidade, o comando para traçar curva parametrizada no DESMOS é o seguinte:
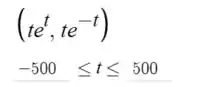
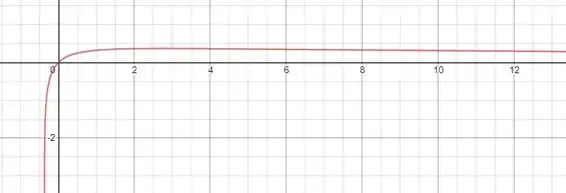
Vendo o gráfico, vemos que o ponto máximo ocorre próximo de enquanto o ponto extremo esquerdo acontece nas proximidades de .
Para encontrar o ponto mais à esquerda na curva, precisamos encontrar o valor de para o qual o gráfico possui uma tangente vertical. Para encontrar o ponto mais alto na curva, precisamos encontrar o valor de para o qual o gráfico possui uma tangente horizontal.
Então deveremos derivar e em relação a , e para encontrarmos tangente horizontal, deveremos ter:
E
Sendo então esse o ponto mais ‘alto’.
Já para o ponto mais a esquerda, isso irá ocorrer quando
E
Passo 2
Para o ponto mais alto:
Utilizando a regra do produto:
Agora iremos zerar:
Então temos que o ponto mais alto é:
Para
Passo 3
Para o ponto mais à esquerda:
Agora vamos zerar:
Então temos que o ponto mais à esquerda é:
Para
Passo 4
Para as assíntotas, precisamos verificar o comportamento da função quando se aproxima de mais ou menos infinito.
Usando a Regra de L'Hôpital, temos que tende a infinito para e tende a menos infinito para , então o eixo e o eixo são assíntotas, respectivamente.
