Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.21 - Ex. 22

Mostre que as curvas equações são 2 x 2 + 3 y 2 = 5 e y 2 = x 3 interceptam-se no ponto ( 1,1 ) e que suas tangentes nesse ponto são perpendiculares.

Passo 1

Vamos começar verificando a interseção...

2 x 2 + 3 y 2 = 5 y 2 = x 3

Substituindo uma na outra...

2 x 2 + 3 x 3 = 5

O ponto ( 1,1 ) satisfaz a equação...

2 1 2 + 3 1 2 = 5

5 = 5

Então, as curvas se interceptam no ponto ( 1,1 ) .

Passo 2

Vamos ver as tangentes agora.

Derivando a primeira...

4 x + 6 y y ' = 0

y ' =   - 4 x 6 y

y ' =   - 2 x 3 y

A equação da reta tangente no ponto ( 1,1 ) dessa reta então é:

y - 1 = - 2 3 x - 1

Passo 3

E agora a segunda...

2 y   y ' = 3 x 2

y ' = 3 x 2 2 y

E a equação da reta tangente no ponto ( 1,1 ) aqui é:

y - 1 = 3 2 ( x - 1 )

Passo 4

Os coeficientes angulares das duas retas tangentes são opostos e inversos, isso quer dizer que as duas retas são perpendiculares.

Vamos só ver isso no gráfico agora...

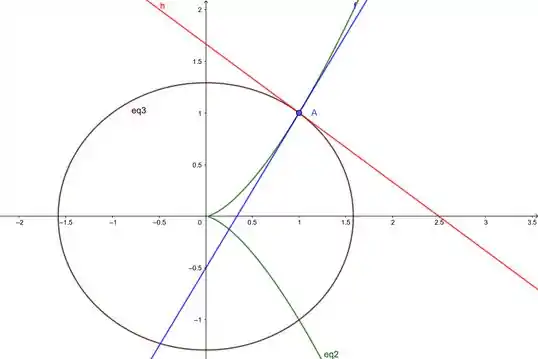
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre d 2 y / d x 2 por derivação implícita. y + sin ⁡ y = x
Use diferenciação implícita para encontrar a derivada especificada. a 4 - t 4 = 6 a 2 t , d a / d t
Use diferenciação implícita para encontrar a derivada especificada. a 2 ω 2 + b 2 λ 2 = 1 , d ω / d λ
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A função | x | não está definida implicitamente pela equação x + y x - y = 0
Use diferenciação implícita para encontrar a inclinação da reta tangente à curva no ponto especificado e verifique se sua resposta está de acordo com o gráfico. y 3 + y x 2 + x 2 - 3 y 2 = 0 ; ( 0 , 3