- Mostre graficamente que são linearmente independentes em
- Mostre que para todo número real.
Passo 1
E aí, tudo bem?
- Vamos esboçar os gráficos das funções:
- Agora vamos ver que:
:
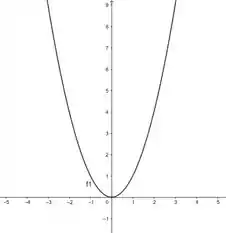
E :
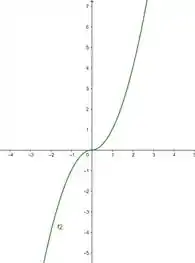
Podemos ver que não tem como essas duas funções serem múltiplas, daí a gente vê que elas são linearmente independentes!
Passo 2
Vamos calcular o Wronskiano então. Primeiro para :
E agora para :
Assim, provamos que para todo número real 😉

Resposta
Ei, a resposta está no passo a passo :)