Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 21

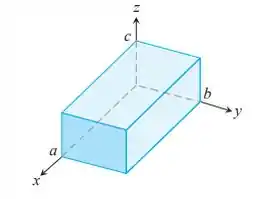
Momentos de inércia: encontre os momentos de inercia do sólido retangular mostrado aqui com relação as suas arestas calculando I x ,   I y ,   I z .

Passo 1

Faaaala, cara! Tranquileba?

Temos pela figura que:

x ∈ 0 , a

y ∈ 0 , b

z ∈ [ 0 , c ]

E todos são perpendiculares entre si, então é válido a gente usar o teorema dos eixos perpendiculares, onde:

I z = ∭ x 2 + y 2 d x   d y   d z  

I x = ∭ y 2 + z 2   d x   d y   d x  

I y = ∭ x 2 + z 2 d x   d y   d x

Assim, usemos para I x . Então temos:

I x = ∫ 0 a ∫ 0 b ∫ 0 c y 2 + z 2   d z   d y   d x

Passo 2

I x = ∫ 0 a ∫ 0 b ( y 2 z 0 c + 1 3 z 3 0 c )   d y   d x

∫ 0 a ∫ 0 b y 2 c + c 3 3 d y   d x

∫ 0 a c 3 y 3 0 b + c 3 3 y 0 b d x

∫ 0 a c b 3 3 + c 3 b 3 d x

c b 3 + c 3 b 3 x 0 a

c b 3 a + c 3 b   a 3

a b c 3 b 2 + c 2

I x = M 3 b 2 + c 2

Onde M = a b c

Passo 3

M 3 b 2 + c 2

Onde M = a b c .

Para I y :

I y = ∫ 0 a ∫ 0 b ∫ 0 c x 2 + z 2 d z   d y   d x

∫ 0 a ∫ 0 b x 2 z 0 c + 1 3 z 3 0 c d y   d x

∫ 0 a ∫ 0 b x 2 c + c 3 3 d y   d x

∫ 0 a x 2 c y 0 b + c 3 3 y 0 b d x

∫ 0 a x 2 c b + c 3 b 3 d x

c b 3 x 3 0 a + c 3 b 3 x 0 a

c b a 3 3 + c 3 b a 3

a b c 3 a 2 + c 2

I y = M 3 a 3 + c 2

Onde M = a b c .

Para I z :

I z = ∫ 0 a ∫ 0 b ∫ 0 c x 2 + y 2 d z   d y   d x  

∫ 0 a ∫ 0 b x 2 + z 2 z 0 c   d y     d x

∫ 0 a ∫ 0 b x 2 + y 2 c   d y   d x

∫ 0 a c x 2 y 0 b + c 3 y 3 0 b d x

∫ 0 a c x 2 b + c b 3 3 d x

c b 3 x 3 0 a + c b 3 3 x 0 a

c b a 3 3 + c b 3 a 3

a b c 3 a 2 + b 2

I z = M 3 a 2 + b 2

Onde M = a b c .

Resposta

I x = M 3 b 2 + c 2

I y = M 3 a 3 + c 2

I z = M 3 a 2 + b 2

(Onde M = a b c )  

Exercícios de Livros Relacionados

Utilize coordenadas esféricas.a) Determine o centroide do hemisfério sólido homogêneo de raio a .b) Determine o momento de inércia do sólido da parte (a) em relação a um diâmetro de sua base.
a) Determine o centroide de um cone circular reto com altura h e base com raio a. (Coloque o cone de forma que a base esteja sobre o plano x y com o centro na origem e seu eixo esteja sobre o eixo z.)
(a) Encontre o centroide do sólido no Exemplo 4 .(b) Encontre o momento de inércia em torno do eixo z para este sólido.
Determine os momentos de inércia para um cubo com densidade constante k e lados de comprimentoL se um vértice está localizado na origem e três arestas estão nos eixos coordenados.
Determine os momentos de inércia do tijolo retangular de dimensões a , b e c , massa M e densidade constante se o centro do tijolo está na origem e suas arestas são paralelas aos eixos coordenados