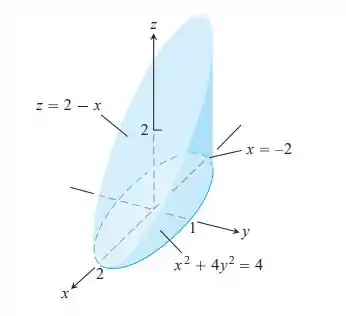
Para M:
Façamos logo , e quando e para Assim:
Sabemos que , logo
E novamente usando que , logo
E usando da propriedade de que a integral de uma soma é soma das integrais
Para simplificar vamos essa a integral de à parte
E das técnicas de integração, temos que sendo Assim:
Voltando
Sabendo que
Lembrando que
(RAAAAPAZ... que continha trabalhosa)
Para
Para
E usando da propriedade de que a integral de uma soma é soma das integrais
Vamos resolver ambas separadamente.
Para a primeira, façamos logo , e quando e para Assim:
E o processo é semelhante a que nós fizemos para achar a massa. CONTUDO, veja que esta é uma função impar e participante em um intervalo simétrico.
SE UMA FUNÇÃO É IMPAR E SEU INTERVALO DE INETGRAÇÃO É SIMETRICO, OU SEJA, POR EXEMPLO DE [-1,1], SUA INTEGRAL É 0. Assim:
Para segunda parte:
A segunda parte é uma função parte, feitas as substituições já sabemos que vai dar (comprove, tente fazer a integração)
Assim:
Então: