Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 31
Esboce o gráfico da função.
Passo 1
Fala ai pessoal. Belezinha?
Esta questão basicamente nos pede para plotarmos o gráfico. Para isso vamos utilizar um software, mas antes porque não entender um pouco mais sobre a equação dada.
A função é uma função de duas variáveis que representa uma superfície no espaço tridimensional, que dá altura dá superfície. E dentro da raiz, a equação sugere ter uma simetria elíptica.
Vamos começar! 😊
Passo 2
Vamos entender como a função está definida. Iremos verificar seu domínio.
Elevando ambos os lados ao quadrado
Esta é a equação da elipse no plano , com semieixo maior ao longo do eixo e semieixo menor ao longo do eixo ; O domínio da função é, portanto o interior e a fronteira dessa elipse.
Passo 3
Temos que
No ponto , a altura é máxima:
Nos pontos da fronteira da elipse , a altura é zero:
À medida que nos movemos do centro da elipse para a fronteira, diminui de até .
Essa é a equação da parte de cima de um elipsoide, (porque é sempre positivo aí)...
Passo 4
Imagine uma elipse vertical no plano e no plano , formando uma "tampa" curva que se eleva até no centro.
O gráfico fica assim:
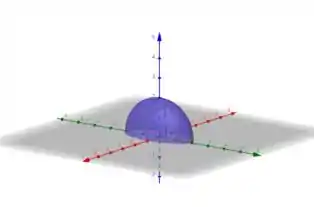
Resposta
