Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 46
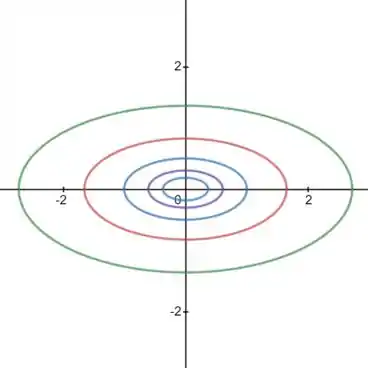
Faça o mapa de contorno da função mostrando várias curvas de nível.
Passo 1
E aí, tudo beleza?
Olha só, para fazer as curvas de nível nós projetamos nossa função no plano, fazendo assim:
Sendo o uma constante qualquer.
Pra a gente saber que tipo de figura vai formar, vamos tirar esse daí, jogando uma exponencial dos dois lados.
Mas calma, é de boa, vem comigo!
Passo 2
Vamos pegar nossa equação ali de cima:
E fazer isso aqui:
Como a gente já sabe, , então aqui, a gente tem:
Que ainda podemos escrever assim:
Agora podemos colocar aquele fator 4 no denominador do segundo termo, aí nossa equação fica:
Lembra dessa equação? É uma elipse, certo?
Passo 3
O centro da elipse é na origem, , e os eixos variam de acordo com o valor de .
Então se , por exemplo, temos a elipse:
Que tem eixos medindo medindo e eixo medindo .
Então as curvas de níveis vão ser uma família de elipses concêntricas, com eixos dependendo de .
Vou fazer aqui com (estão nessa ordem)
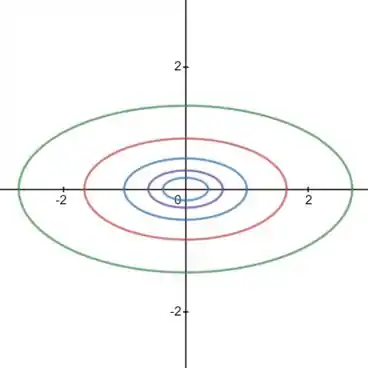
E tá aí o nosso mapa de contorno! 😉
Resposta
