Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 59
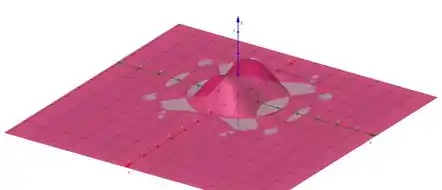
Utilize um computador para traçar o gráfico da função usando vários domínios e pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, trace o mapa de contorno da mesma função e compare.
Passo 1
Olá, meu querido aluno. Vou te acompanhar nessa resolução hoje.
A gente tem a função:
E por meio de um software gráfico deveremos gerar o gráfico da função. Aqui eu estarei utilizando o GeoGebra 3D, ele é online e gratuito então irá nos ajudar bastante.
Estarei te ajudando a lidar com ele, e te ensinar a escolher a visualização que te agradar.
Passo 2
No site GeoGebra 3D, no lado esquerdo da sua tela, você irá inserir a equação da nossa função:
O gráfico gerado será o seguinte:
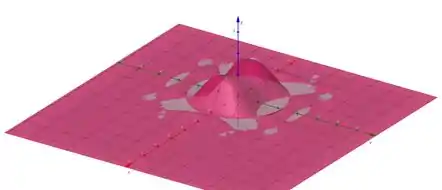
Para que possamos mudar o domínio da nossa função, podemos inserir na mesma aba, uma condição que desejarmos:
Assim poderemos gerar gráficos com diferentes opções de domínio, o gráfico gerado com essa pode ser visto abaixo:
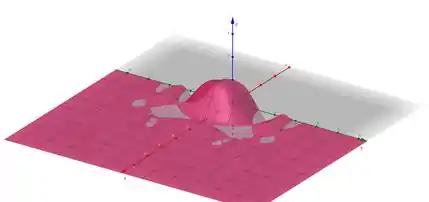
Passo 3
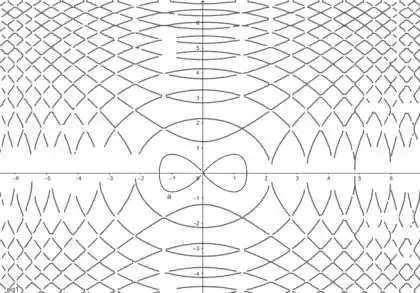
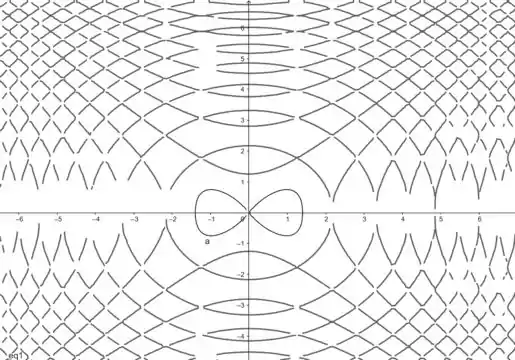
Pra fazer as curvas de nível é só igualar a função a uma constante:
Aí a gente faz igual a alguns valores, tipo . Para plotarmos o gráfico da curva de nível utilizamos o GeoGebra 2D, pois a curva de nível é a planificação do que vemos em 3D.
Resposta
