Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 84
Sob certas circunstâncias, um boato se propaga de acordo com a equação
onde é a proporção da população que já ouviu o boato no instante , e e são constantes positivas.
a) Encontre .
b) Encontre a taxa de propagação do boato.
c) Faça o gráfico de para o caso e , onde é medido em horas. Use o gráfico para estimar quanto tempo será necessário para o boato atingir 80% da população.
Passo 1
E aí! como vai?
O enunciado forneceu uma função que exprime a disseminação de um boato em uma população.
No item (a) é é pedido para determinarmos o limite de quando , isto é, qual a porcentagem da população que terá ouvido o boato depois de muito tempo.
Já no item (b) é pedido a taxa de propagação de boato, para isso basta derivar com relação ao tempo.
E no item (c) temos que esboçar o gráfico de para e e estimar o tempo para o boato chegar em da população.
Bastante coisa, não é?
No item a) basta aplicarmos a função no limite
Já no item b) temos que lembrar que a taxa de variação de uma função é expressa pela sua derivada, logo, temos que determinar a derivada de e para isso podemos aplicar a regra da cadeia que é dada por
E no item c) esboçamos o gráfico de encontrando algumas características da função.
Bora lá!
Passo 2
Neste passo vamos resolver o item (a).
Calculando o limite, vemos que quando , pois . Assim,
Assim, para tempos muito longos se aproxima de , isto é, 100% da população terá escutado o boato (o que faz sentido né?).
Show?
Passo 3
Neste passo vamos resolver o item (b).
A taxa de propagação do boato é a deriva de com relação ao tempo.
Podemos reescrever a função como
Aplicando a regra da cadeia, temos
Perceba que na derivada de estamos derivando em função de , ou seja, tratamos como uma variavel.
Substituindo em ...
Se , então
Tranquilo até aqui?
Passo 4
Agora resolveremos o item (c). Com e , temos que
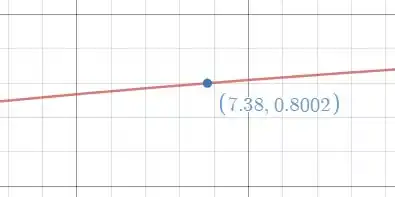
O gráfico de fica:
Note que conforme cresce, se aproxima de , como vimos no item (a).
Olhando no gráfico onde (o que representa 80%) obtemos horas.
E aí! entendeu tudo? Responde Aí!
Resposta
a) .
b) .
c) Esboço de gráfico.