O movimento de uma mola sujeita a uma força de atrito ou a uma força de amortecimento (tal como um amortecedor em um carro) é frequentemente modelado pelo produto de uma função exponencial e uma função seno ou cosseno. Suponha que a equação de movimento de um ponto dessa mola seja
onde é medido em centímetros e , em segundos. Encontre a velocidade após segundos e faça o gráfico das funções posição e velocidade para .
Passo 1
Fala aí! Vamos resolver essa questãozinha juntos!
Bom, nosso enunciado nos dá a função posição de um ponto da mola em movimento amortecido e pede a função velocidade pra gente… Hummm... Vamos pensar um pouquinho… a velocidade a gente costuma encontrar, nos estudos de física, desse jeito, né:
Opa! Então ela é uma função da variação do espaço em relação ao tempo, né? Beleza! Já descobrimos o que precisamos fazer! Temos que derivar a posição com relação ao tempo, tranquilo? Vamos fazer isso então!
Pra derivar isso a gente pode aplicar uma regrinha de derivada… Podemos usar as regras do produto e da cadeia… São duas funções, né? Vamos fazer a derivada da primeira, vezes a segunda, somando a primeira, vezes a derivada da segunda, show? Vamos nessa!
Passo 2
Agora a gente precisa fazer o gráfico da função posição e da função velocidade em , partiu!
Pra fazer isso a gente pode usar um excel para ter mais precisão, ou substituir uma sequência de valores e ver onde vai estar cada ponto, certo?
Nosso gráfico da função posição ficará com essa cara aqui:
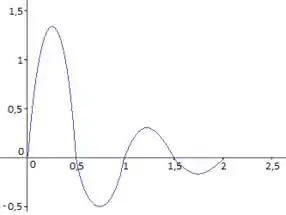
E o gráfico da função da velocidade fica assim, olha só:
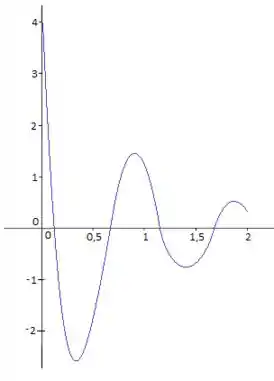
Prontinho! Conseguimos!
Resposta
e Passo 2.