Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.9 - Ex. 8

O movimento de uma partícula é dado por σ t = 3 cos ⁡ t ,   4 s e n t . Calcule o comprimento da componente normal da aceleração no instante t = 0 .

Passo 1

E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D

Pra começarmos esse exercício, precisamos lembrar do conceito de curvatura e do raio de curvatura. Na seção 1.7 do livro Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis - 1ª Ed., o Teorema 1.3 (página 36 ) dessa seção nos dá a fórmula do vetor aceleração:

A t = v ' t T t + v t T ' t N t

Tal que:

A t = σ ' ' t é o vetor aceleração;

v t = V t = σ ' t é a velocidade escalar;

E os coeficientes de T t e N t são, respectivamente, o componente tangencial A T e normal A N da aceleração, ou seja:

A T = v ' t

E:

A N = v t T ' t

Como a aceleração possui esses dois componentes que são perpendiculares entre si e formam um triângulo retângulo (observe a imagem abaixo), ela pode ser definida através do Teorema de Pitágoras:

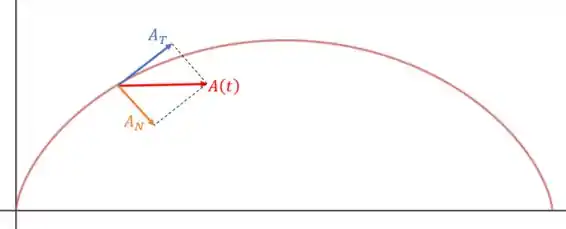
Assim:

A t 2 = A T 2 + A N 2

E, isolando a componente normal:

A N = A t 2 - A T 2

Passo 2

Dessa forma, vamos encontrar a equação geral da aceleração para então verificar as componentes. Tendo a equação:

σ t = 3 cos ⁡ t ,   4 s e n t

Então, derivando-a uma vez, teremos:

σ ' t = - 3 s e n t , 4 cos ⁡ t = V t

E, fazendo isso novamente:

σ ' ' t = - 3 cos ⁡ t , - 4 s e n t = A t

Ainda, a velocidade escalar terá o valor:

v t = σ ' t = - 3 s e n t 2 + 4 cos ⁡ t 2

Logo:

v t = 9 s e n 2 t + 16 cos 2 ⁡ t

Derivando essa função:

v ' t = 18 s e n t cos ⁡ t - 32 s e n t cos ⁡ t 2 9 s e n 2 t + 16 cos 2 ⁡ t

Passo 3

Com esses resultados, torna-se possível fazermos o cálculo que queremos. Como a componente normal é dada por:

A N = A t 2 - A T 2

Teremos:

A t 2 = - 3 cos ⁡ t 2 + - 4 s e n t 2 2

Logo:

A t 2 = 9 cos 2 ⁡ t + 16 s e n 2 t

E:

A T 2 = 18 s e n t cos ⁡ t - 32 s e n t cos ⁡ t 2 9 s e n 2 t + 16 cos 2 ⁡ t 2

Passo 4

Assim, substituindo na fórmula da componente normal:

A N t = 9 cos 2 ⁡ t + 16 s e n 2 t - 18 s e n t cos ⁡ t - 32 s e n t cos ⁡ t 2 9 s e n 2 t + 16 cos 2 ⁡ t 2

Mas como o exercício pede para encontrar o resultado no instante t = 0 , obtemos:

A N 0 = 9 cos 2 ⁡ 0 + 16 s e n 2 0 - 18 s e n 0 cos ⁡ 0 - 32 s e n 0 cos ⁡ 0 2 9 s e n 2 0 + 16 cos 2 ⁡ 0 2

Portanto:

A N 0 = 9 = 3

Resposta

A N 0 = 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se no plano de modo que, no instante t , sua posição é dada por: r → t = 2 cos ⁡ t 2 ,2 s e n t 2 Calcular o vetor u → t = v → t v → t , onde v → ( t ) é o vetor velocidade da partí
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:3)σ t = e 2 t , t 2 , t 1 = 0 a) o vetor velocidade V t ;
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:4)σ t = cos ⁡ t , sen ⁡ t , 2 , t 1 = π 2 a) o vetor velocidade V t ;
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:2)σ t = cos ⁡ 2 t , - 3 sen ⁡ t , t 1 = π c) a velocidade escalar em t =
Nos exercícios de 1 a 6 , σ t denota o vetor posição de uma partícula se movendo, em cada instante t . Em cada caso, determine:3)σ t = e 2 t , t 2 , t 1 = 0 c) a velocidade escalar em t = t 1