Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.7 - Ex. 36
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessitará da relação .
Uma corredora dos arranca com uma aceleração de , a qual mantém por segundos. Sua aceleração, então, cai para zero pelo restante da prova.
(a) Qual foi o seu tempo de corrida?
(b) Faça um gráfico da distância a partir da arrancada versus tempo.
Passo 1
(a) Para descobrir o tempo total de corrida, precisamos descobrir quantos metros ela correu sem aceleração, descobrindo quantos metros ela correu nos primeiros e substraindo isso dos .
Sendo:
Vamos usar a fórmula:
Isso quer dizer que ela correu em . Agora vamos descobrir quanto tempo levou para ela correr os últimos .
Passo 2
Para fazer isso, precisamos descobrir também a velocidade que ela atingiu ao acelerar e que continuou a ser a velocidade dela sem a aceleração. É só descobrir a velocidade final da primeira parte do trajeto pela fórmula:
Sendo:
Achamos:
Passo 3
Agora temos todos os dados. Como nos últimos não houve mudança de velocidade, podemos dizer que:
Sabemos que:
Logo,
O tempo total de corrida é:
Passo 4
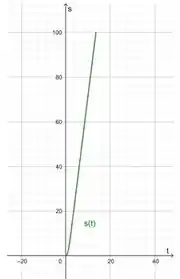
(b) Para fazer esse gráfico, precisamos montar a função:
Para e , porque esses períodos tem acelerações diferentes.
Para o primeiro, , . Então:
Para o segundo, , , , . Podemos usar:
Chamando , e usando nossos dados:
Passo 5
Agora é só a gente esboçar a função:
Fica assim, oh:
