Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.3 - Ex. 38
Um objeto de massa é arrastado ao longo de um plano horizontal por uma força agindo ao longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a intensidade da força é
Onde é uma constante chamada coeficiente de atrito.
(a) Encontre a taxa de variação de em relação a .
(b) Quando essa taxa de variação é igual a ?
(c) Se , e , faça o gráfico de como uma função de e use-o para localizar o valor para o qual . Esse valor é consistente com a resposta dada na parte (b)?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
Parece física, mas é cálculo, não se assusta! O problema nos diz que um objeto de massa é arrastado ao longo de um plano horizontal por uma força.
Se a corda faz um ângulo com o plano, então a intensidade da força é:
Onde é uma constante chamada coeficiente de atrito.
A primeira coisa que o problema quer que a gente faça é achar a taxa de variação em relação a . Quando a gente ouve taxa de variação, significa que deveremos derivar. Nesse caso aqui, a gente tem que derivar em relação a , usando a regra do quociente, beleza?! Pois temos um quociente de funções a serem derivadas.
Pela regra do quociente temos que:
Depois, vamos descobrir quando essa taxa de variação é igual a zero, fazendo e encontrando o valor de .
Por fim, vamos fazer , e , na nossa função, esboçar o gráfico de como uma função de e usá-lo para localizar o valor para o qual , verificando se valor é consistente com a resposta dada na parte (b).
Vamos lá!
Passo 2
Vamos começar derivando a nossa função, usando a regra do quociente:
Primeiro vamos jogar pra fora tudo que for constante, pois podemos retirar as constantes da derivação, pra facilitar nossa vida:
Então, aplicando a regra do quociente, nossa função vai ficar:
Realizando as derivadas do e do :
Simplificando:
Passo 3
Na letra (b) a gente quer saber quando essa taxa é igual a , então vamos fazer :
são constantes definidas, então elas são diferentes de zero e o denominador tem que ser diferente de zero também, concorda?!
O que sobra pra a gente, então, é:
Com isso podemos fazer:
Isolando :
E usando a identidade trigonométrica vamos ter:
Logo, essa taxa só será nula quando .
Passo 4
Por fim, a gente tem a letra (c), que dá os seguintes dados pra a gente:
, e
E pede o gráfico de como uma função de e a localização de , para confirmar a resposta da letra (b)!
Então vamos lá!! Substituindo os dados em:
Temos:
Portanto, temos o gráfico:
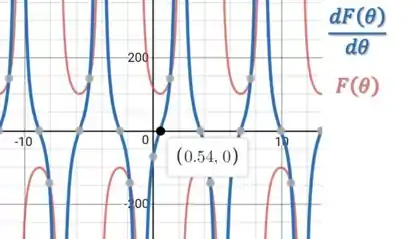
E esse valor é consistente com a resposta dada na parte (b) pois:
Valeu, galera! Até a próxima! 😉
Resposta
(a) .
(b) Essa taxa só será nula quando .
(c) Esse valor é consistente com a resposta dada na parte (b) pois: