Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 65

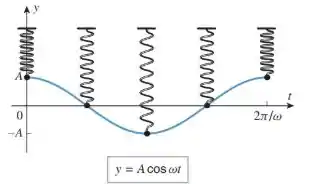
Um objeto suspenso por uma mola e em repouso sofre um pequeno deslocamento vertical e depois é abandonado. Se forem ignoradas a resistência do ar e a massa da mola, então a oscilação do objeto é chamada de movimento harmônico simples. Sob condições apropriadas, o deslocamento y do equilíbrio em termos do tempo t é dado por

y = A cos ⁡ ω t

onde A é o deslocamento inicial em t = 0 e ω é uma constante que depende da massa do objeto e da rigidez da mola (ver figura abaixo). A constante |A| é denominada a amplitude do movimento e ω é a frequência angular.

  1. Mostre que

    2. d 2 y d t 2 = - ω 2 y

  2. O período T é o tempo necessário para fazer uma oscilação completa. Mostre que

    3. T = 2 π ω

  3. A frequência f de vibração é o número de oscilação por unidade de tempo. Encontre f em termos do período T .
  4. Encontre a amplitude, o período e a frequência de um objeto executando um movimento harmônico simples, dado por y = 0,6 cos ⁡ 15 t , onde t está em segundos e y , em centímetros.

Passo 1

  1. Para mostrar que a equação dada é verdadeira, vamos derivar duas vezes a função y . Para tal, vamos usar a regra da cadeia. Seja u = ω t . Assim,

    2. d y d t = d y d u d u d t d y d t = d d u A cos ⁡ u d d t ω t d y d t = - A sin ⁡ u ⋅ ω d y d t = - A ω sin ⁡ u

    Como u = ω t , segue que

    d y d t = A   ω sin ⁡ ω t

    Derivando mais uma vez e fazendo, novamente, u = ω t :

    d 2 y d t 2 = d d u - A ω sin ⁡ u d d t ω t d 2 y d t 2 = - A ω cos ⁡ u ω d 2 y d t 2 = - A ω 2 cos ⁡ u d 2 y d t 2 = - A ω 2 cos ⁡ ω t

    Porém, notemos que

    y = A cos ⁡ ω t

    Logo,

    d 2 y d t 2 = - ω 2 A cos ⁡ ω t d 2 y d t 2 = - ω 2 y

    Passo 2

  2. Temos y t = A cos ⁡ ω t . O período T é definido como sendo o menor instante de tempo tal que:

    3. y t + T = y t A cos ⁡ ω t + T = A cos ⁡ ω t cos ⁡ ω t + ω T = cos ⁡ ω t

    Lembrando que cos ⁡ x = cos ⁡ y então x = y + 2 k π , onde k é um número inteiro, então:

    ω t + ω T = ω t + 2 k π ω T = 2 k π T = 2 k π ω

    Para que T seja o menor possível, devemos escolher k = 1 . Assim,

    T = 2 π ω

    Passo 3

  3. Note que:

    4. T é o intervalo de tempo necessário para que uma oscilação seja dada

    Assim, se em um tempo Δ t foram realizadas n oscilações, então o período T é dado por:

    T = Δ t n

    f é o número de oscilações por intervalo de tempo

    Assim, se n oscilações são dadas em um intervalo de tempo Δ t , então a frequência f é dada por:

    f = n Δ t

    Multiplicando f por T , teremos:

    f T = n Δ t Δ t n f T = 1

    Ou seja,

    f = 1 T

    Passo 4

  4. Vamos comparar a equação dada y = 0,6 cos ⁡ 15 t com a equação geral y = A cos ⁡ ω t .

Vemos que:

A = 0,6   c m

ω = 15     r a d / s

Portanto,

  • A amplitude vale 0,6   c m .
  • O período vale T = 2 π ω = 2 3,14 15 ≈ 0,42   s .
  • A frequência irá valer f = 1 T ≈ 2,39   s

Resposta

  1. Demonstração.
  2. T = 2 π / ω .
  3. f = 1 / T .
  4. A = 0,6   c m ;     T = 0,42   s ;     f = 2,39   s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Derivada de cos ⁡ ( x 2 ) . Represente graficamente a função y = - 2 x sen ⁡ x 2 para - 2 ≤ x ≤ 3 . Depois, na mesma tela, faça o gráfico de y = cos ⁡ x + h 2 - cos ⁡ ( x 2 ) h Para h = 1.0 ; 0 . 7 e0
Coeficientes angulares de senoidesDetermine as equações para as tangentes às curvas y = sen ⁡ 2 x e y = - sen ⁡ x / 2 na origem. Existe algum aspecto diferente no modo como essas tangentes estão relac
Coeficientes angulares de senoidesDetermine as equações para as tangentes às curvas y = sen ⁡ 2 x e y = - sen ⁡ x / 2 na origem. Existe algum aspecto diferente no modo como essas tangentes estão relac
Coeficientes angulares de senoidesDetermine as equações para as tangentes às curvas y = sen ⁡ 2 x e y = - sen ⁡ x / 2 na origem. Existe algum aspecto diferente no modo como essas tangentes estão relac
Coeficientes angulares de senoidesDetermine as equações para as tangentes às curvas y = sen ⁡ 2 x e y = - sen ⁡ x / 2 na origem. Existe algum aspecto diferente no modo como essas tangentes estão relac