Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 11
Trace ou copie o gráfico de . (Suponha os eixos da mesma escala). Use então o método do Exemplo para esboçar o gráfico de .
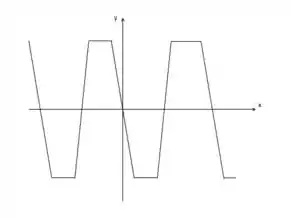
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente usar o gráfico da função dada para esboçar o gráfico da derivada , de acordo com o método do Exemplo .
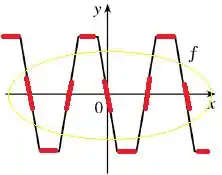
O gráfico dado foi esse aqui:
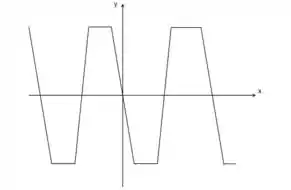
O método do exemplo consiste em traçarmos retas tangentes em alguns pontos da nossa curva e analisar a inclinação dessas retas. A partir disso, saberemos se a derivada da função em cada ponto é positiva, negativa ou nula e conseguiremos traçar uma curva para .
Então, é isso que nós vamos fazer. Vamos lá!
Passo 2
Já sabemos que é possível estimar o valor de qualquer derivada de , traçando a reta tangente a e estimando a sua inclinação. Então, vamos traçar algumas retas no nosso gráfico:
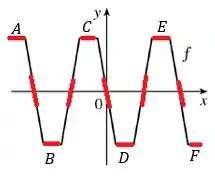
Observe que os pontos e têm retas tangentes horizontais, o que significa que elas possuem inclinação nula e, portanto, a derivada nesses pontos é zero. Como ela é zero, ela vai ser uma reta horizontal no eixo :
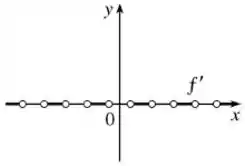
As bolinhas vazias representam os pontos onde a função não está definida. Isso acontece por conta das “quinas” que aparecem na função .
Lembre-se que, em geral, se o gráfico de uma função tiver uma “quina” ou uma “dobra”, então o gráfico de não terá tangente nesse ponto, e não será diferenciável ali (a derivada não existe no ponto).
Passo 3
Beleza, mas o gráfico ainda não está completo. Observe que temos alguns pontos onde a nossa função é decrescente e as retas tangente têm inclinação negativa e pontos onde a função é crescente e as retas passam a ter inclinação positiva. Observe também que independente do sinal, essas inclinações são constantes:
Nos locais onde a inclinação é positiva, a nossa derivada é positiva e estará acima do eixo . Nos locais onde a inclinação é nagativa, a nossa derivada é negativa e estará abaixo do eixo . Mas em ambos os casos, como elas são constantes em cada ponto, elas serão representadas por linhas horizontais.
Assim, temos o gráfico de :
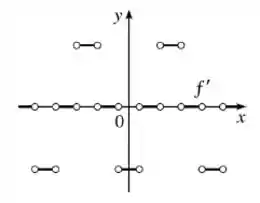
Valeu, galera! Até a próxima! 😉
Resposta
Gráfico de