Olhando para o gráfico de , estude o sinal de .
Passo 1
Nesta função, a reta emcontra o eixo no ponto e encontra o eixo no ponto . Assim, pode ser esboçada como:
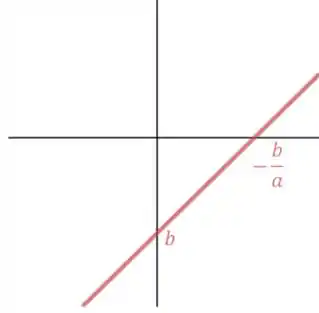
Passo 2
Podemos ver que a reta cruza o eixo dos no ponto e por ser crescente, antes desse ponto só temos valores de menores que zero de depois de todo os valores são maiores que zero. Então:
para
para
Resposta
para
para