Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 4
Para a parábola, ache as coordenadas do foco, a equação da diretriz e o comprimento do latus rectum. Faça um esboço da parábola.
Passo 1
O exercício da a equação de uma parábola com vértice na origem (se não apareciam termos com e ) e pede para determinar todos os elementos que caracterizam a parábola: foco, reta diretriz e um esboço. Como a equação é do tipo
o eixo de simetria da parábola é o eixo . Assim, a reta diretriz será paralela ao eixo .
Neste caso, temos. Assim, o foco, que estará sobre o eixo (eixo de simetria) estará abaixo da parábola, de modo que a reta diretriz estará acima!
Passo 2
Como o eixo de simetria é o eixo , o foco é dado por e a reta diretriz por . Assim, temos que
Por fim, o comprimento do latus rectum é dado por , de modo que .
Passo 3
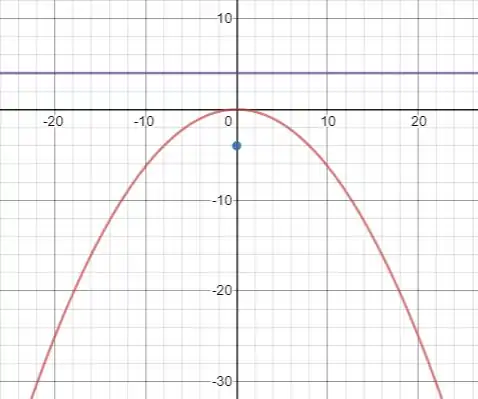
Um esboço da parábola é dado a seguir:
