Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 20

Uma pérola no xampu. Suponha que uma pérola esteja afundando em um líquido denso, como xampu, sujeita a uma força de atrito oposta à sua queda e proporcional à sua velocidade. Suponha que também exista uma força de empuxo exercida pelo xampu. De acordo com o princípio de Arquimedes, a força de empuxo é igual ao peso do líquido deslocado pela pérola. Usando m para a massa da pérola e P para a massa do xampu deslocada pela pérola enquanto ela afunda, execute as etapas a seguir.

  1. Faça um diagrama esquemático em que sejam mostradas as forças que agem sobre a pérola enquanto ela afunda, como o que vemos na Figura 9 .19.
  2. Usando v ( t ) para a velocidade da pérola em função do tempo t , escreva uma equação diferencial que modele a velocidade da pérola como a de um corpo em queda.
  3. Construa uma reta de fase em que sejam mostrados os sinais de v ' e v " .
  4. Esboce curvas integrais típicas.
  5. Qual é a velocidade terminal da pérola?

Passo 1

O diagrama de corpo livre que ilustra a situação problema é

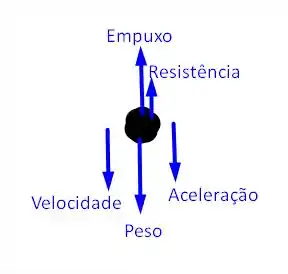
Onde,

F e m p u x o = P g ,

a = d v d t ,

F r e s i s t ê n c i a = k v

P e s o → W = m g

Passo 2

Usando a segunda lei de Newton e somando as forças na direção da aceleração teremos

m g - P g - k v = m a → d v d t = m - P m ⋅ g - k v m

Passo 3

Achando os pontos de equilíbrio, teremos

m - P m ⋅ g - k v m = 0

m - P m ⋅ g = k v m

m - P ⋅ g = k v

v t e r m i n a l = m - P ⋅ g k

Analisando a concavidade (segunda derivada) teremos

d 2 v d t 2 =   - k m ⋅ d v d t =   - k m 2 ⋅ m - P ⋅ g k - v

Dessa forma, nossa reta de fase será dada por

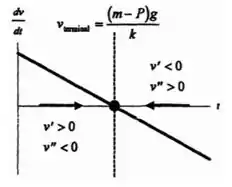
Passo 4

A curva integral será dada por uma curva que tende a crescer até o valor da velocidade terminal que será uma reta horizontal assintótica

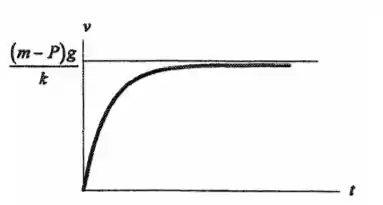
Passo 5

A velocidade terminal da pérola é dada por

v t e r m i n a l = m - P ⋅ g k

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um foguete é lançado da superfície da terra verticalmente para cima. Depois de esgotado todo o combustível, a massa do foguete é constante igual a m . Use a segunda lei de Newton para o movimento e o
Um barril em forma cilíndrica, com s metros de diâmetro e w newtons de peso, flutua na água. O barril se movimenta para cima e para baixo ao longo de uma linha vertical. Usando a figura 1.23(b), deter
A segunda lei de Newton F = m . a pode ser escrita como F = d d t ( m . v ) . Quando a massa de um objeto não é constante, esta última formulação é usada. A massa m ( t ) de um foguete muda enquanto s
Uma pessoa P, partindo da origem, move-se na direção positiva do eixo x, puxando um peso ao longo da curva C (chamada tratriz), como mostrado na figura 1.24. O peso, inicialmente localizado no eixo y
Uma curva C no plano reflete os raios de luz de tal modo que todo raio L paralelo ao eixo y é refletido para um único ponto 0. Determine a equação diferencial para a função y = f ( x ) que descreve a