Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 11
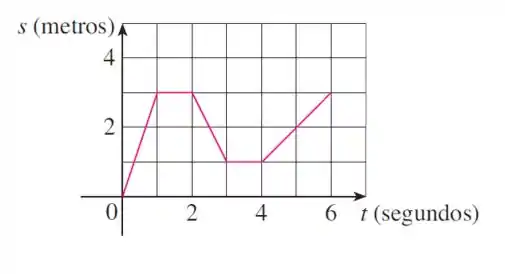
- Uma partícula começa se movendo para a direita ao longo de uma reta horizontal; o gráfico de sua função posição está mostrado. Quando a partícula está se movendo para a direita? E para a esquerda? Quando está parada?
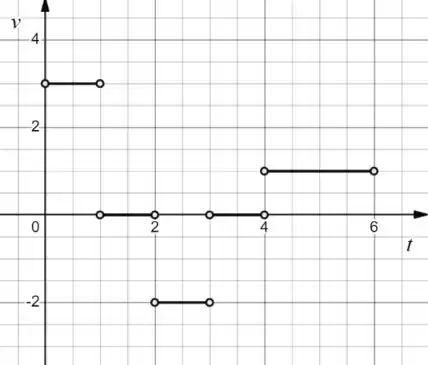
- Trace um gráfico da função velocidade
Passo 1
Olá, meu nobre amigo. Yuri aqui estarei te ajudando a resolver essa atividade.
Vamos lá! O problema da um gráfico pra a gente da posição de uma partícula em função do
tempo:
E a partir disso, ele pergunta na letra a, quando que a partícula esta se movimentando pra esqueda e quando ela esta indo pra direita e diz que uma particula começa se movendo para a direita ao longo de uma reta horizontal:
Se a gente ta falando que ela ta caminhando para o lado direito a gente ta convencionando que o lado direito é o “andar pra frente” e o lado esquerdo é “voltar”, concorda?!
Passo 2
Com isso em mente, o eixo do grafico nos da a posição, então quando o gráfico apresenta uma reta crescente significa que a particula ta andando “para frente”, logo para direita. Da mesma forma, uma reta decrescente significa que a particula esta andando para a esquerda!
Por fim, quando o gráfico apresenta uma reta horizontal é porque a distância não esta mudando, logo a partícula esta parada!
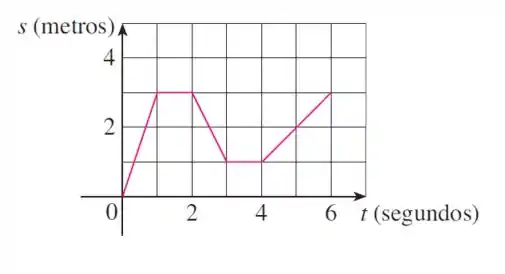
Observando o gráfico:
- Nos intervalos a partícula está se movendo para a direita.
- Nos intervalos a partícula está parada.
- No intervalo a partícula está se movendo para a esquerda.
Passo 3
Na letra (b) precisamos traçar um grfico da velocidade em função do tempo. A velocidade média da partícula é dada por:
E graficamente a velocidade média é a inclinação de cada reta do gráfico, então toda vez que a inclinação muda, a velocidade ta mudando!
Então, calcularemos as velocidades nos intervalos de tempos definidos no item (a)
- Para a velocidade é dada por:
- Para :
- Para :
- Para :
- Para :
Agora, plotaremos um gráfico com as informações obtidas
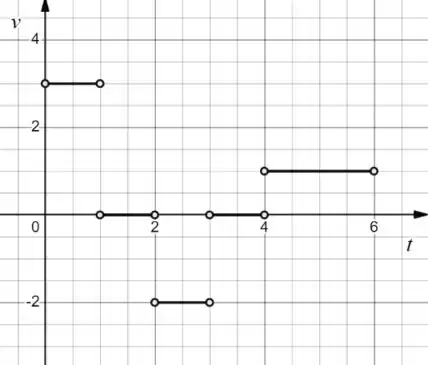
Aparece aqui uma velocidade negativa, que é referente ao momento que a partícula caminha para a esquerda!
Resposta
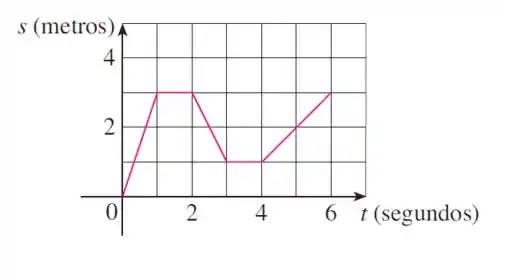
(a)
- Nos intervalos a partícula está se movendo para a direita.
- Nos intervalos a partícula está parada.
- No intervalo a partícula está se movendo para a esquerda.
(b)
