Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.14 - Ex. 8b
Uma partícula se move no espaço com vetor posição . Determinar a velocidade e a aceleração da partícula em um instante qualquer. Esboçar a trajetória da partícula e os vetores velocidade e aceleração para os valores indicados de .
b)
Passo 1
Nessa questão temos que lembrar das coisas que aprendemos lá em física: A velocidade é a derivada do espaço e a aceleração é a derivada da velocidade. Show? Então vem comigo!
O vetor posição é o seguinte:
Então para acharmos a velocidade, basta derivarmos . Derivando,
Isto é,
Passo 2
Para encontrarmos o vetor aceleração, vamos derivar . Assim,
A derivada desse primeiro termo fica o seguinte:
Assim,
Então o vetor aceleração fica assim:
Passo 3
Agora vamos encontrar da velocidade nos instantes e .
No instante :
Logo,
No instante :
Isto é,
Passo 4
Já para aceleração, temos o seguinte:
Em :
Em :
Passo 5
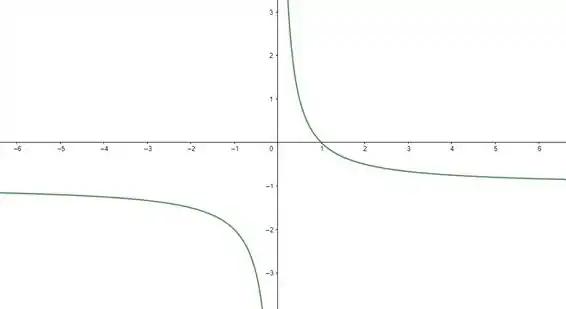
Por fim, vamos fazer um esboço da trajetória da partícula.
Fazendo um esboço:
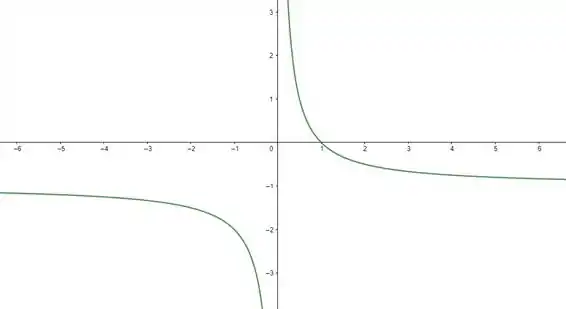
Resposta
Para qualquer instante :
Para :
Para :
Esboço da trajetória:
