Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 4
Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva .
Onde é a curva obtida como interseção do parabolóide com o plano .
Passo 1
Faalaa Zezé, bom dia cara.... Tudo pronto aí pra mais uma questãozinha de Stokes? Só vamo!
Não tem jeito, a gente precisa esboçar esses caras pra tentar achar a queridinha curva:
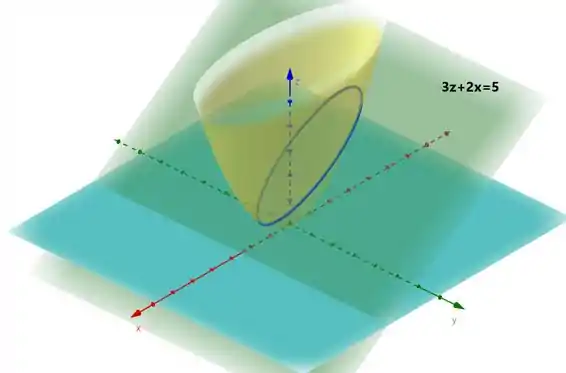
Aquele negocinho em azul é justamente a nossa cuja dita curva . Vamos isolar ela pra dar uma despoluída no desenho:
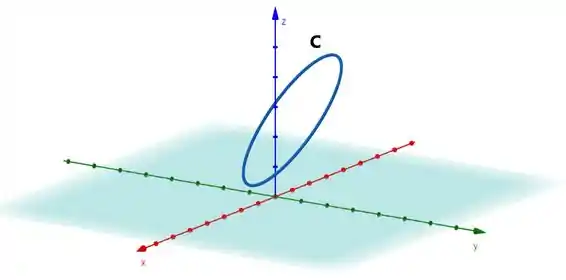
Beeleza; então é sob essa curva que:
Mas queremos provar se isso é verdade, para tanto devemos utilizar o teorema de Stokes, que diz o seguinte:
Ou seja, o teorema transforma a integral de linha para uma integral de superfície. Mas quem é essa superfície?? A mais simples das possibilidades é:
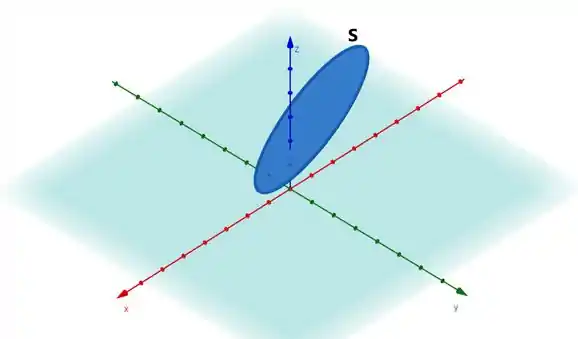
Consegue notar a diferença entre a curva e a superfície ?? É sutíl mas é importante.
Beleza, então é sob essa superfície que vamos trabalhar.
Passo 2
Para poder tacar tudo na integral, precisamos achar aqueles caras lá.
Vamos começar com o rotacional; se você tiver com a memória em dia saberá que a gente encontra esse cara assim:
Onde:
Captou a ideia? Só precisamos encontrar essas derivadas parciais:
E
Top demais, então o tal ro rotacional é definido assim:
Agora a outra criatura que precisamos para tacar na integral é o vetor normal. Perceba que o vetor normal a nossa superfície é na verdade normal ao plano. Olha só:
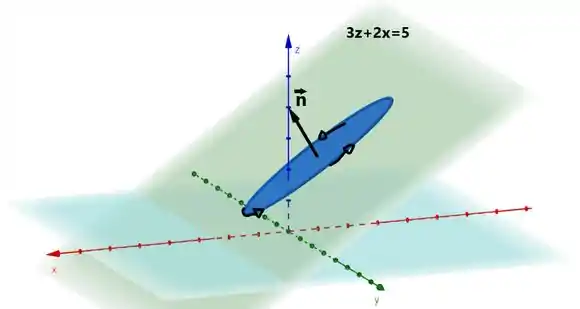
Já aproveitando para supor uma orientação da borda da nossa superfície. Uma vez definida a orientação (anti-horário) podemos encontrar o sentido do vetor normal.
Com a mão direita coloca ela na tela; faz o sinal de “jóia” , com os outros 4 dedos você percorre a curva no sentido que definimos, ou seja, faça com que os seus dedos tentem entrar na tela. Percebeu que seu dedão ta meio que na diagonal apontando pra lá esquerda? É esse o sentido do nosso vetor normal.
Beleza, mas como a gente define esse cara?? Então, encontrar um vetor normal a um plano é bem tranquilo, olha só:
“Seja um plano genérico: , O vetor normal a esse cara será: ”
Pegou a ideia?? Trazendo isso pro nosso problema, encontramos o seguinte vetor normal:
Show dibola.
Passo 3
Agora sim, finalmente podemos tacar tudo na integral:
E fazendo o produto vetorial ali:
Tirando a constante:
Perceba que uma integral dupla daquele cara alí é a area de algo. Mas não pode ser a area no espaço, tem que ser a area de algo no plano pois a integral é dupla.
Com isso devemos projetar essa superfície em algum plano. Se optarmos pelo clássico plano teremos o seguinte:
Onde é a projeção em questão. Sabemos que a projeção será dada pela interseção do parabolóide com o plano; então:
Se somarmos 1 em cada lado da igualdade:
Repara que podemos simplificar assim:
Passando o 6 dividindo:
Percebe o que é essa criança?? Isso mesmo uma elipse!
Isso significa que a projeção da nossa superfície no plano é uma elipse com e .
Se você tiver ligadasso comigo sabe que tudo o que precisamos é da area dessa elipse... lembra como a gente acha isso??
É bem tranquilo, é só você pensar que a elipse é uma circunferência só que com dois tamanhos para o raio...
Se a area da circunferência é vezes raio, a elipse vai ser vezes raio 1 vezes raio 2; ou seja:
Portanto:
Concluindo:
Poxa vida cara, mas não é isso aínão... o enunciado queria que fosse negativo!!
Siimm muito beem!! Você ta atento ao rolê!
A única questão é que o enunciado tomou outra orientação para o vetor normal. Ou seja, ele escolheu:
O enunciado optou pelo sentido horário, então basta que a gente altere o sinal da resposta.
É só isso!
Resposta
Concluindo, é verdade que:
Onde é orientada no sentido horário!!