Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 6

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva .

Onde é a interseção do plano com o cilindro

Passo 1

Seguimos na nossa luta em entender o tal do Stokes. Vamos juntos matar mais um exercise!

Não tem escapatória, a gente precisa enxergar a tal curva; vamos ter que esboçar essa criatura:

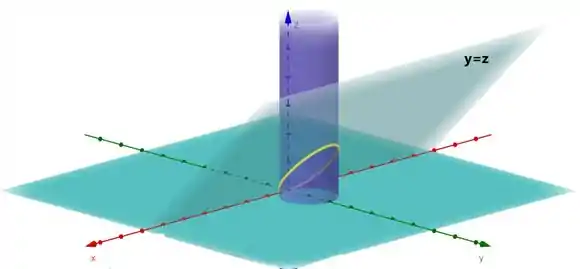
Então a nossa curvinha é aquela em amarelo alí. Vamos retirar tudo que a gente não precisa e já vamos definir um sentido de orientação pra ela:

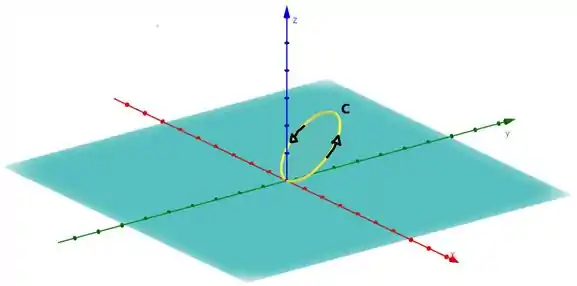
Então é sob essa curva que o exercício diz:

Serase mesmo?? Vamos comfirmar isso. Podemos utilizar Stokes:

Beleza? Só que se quisermos utilizar o teorema não podemos mais trabalhar sob a curva , agora a gente precisa definir uma superfície. Ela pode ser a seguinte:

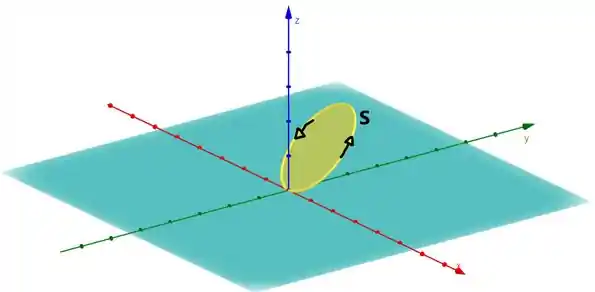
Consegue notar a diferença?? Sim, a superfície tem um preenchimento ali, a curva passa a ser só a borda da nossa superfície.

Beleza, tendo isso em mente podemos encontrar os carinhas que precisamos para calcular a integral.

Passo 2

De praxe, vamos começar pelo rotacional; lembrando que:

Onde:

Só precisamos então encontrar essas derivadas parciais. Bora!

Oras bolas,

É isso mesmo produção? Parece que sim...

Passo 3

Então sem segredos:

E isso comfirma o que diz o enunciado:

É só correr pro abraço!

Resposta

Demonstrado:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y cos ⁡ z i → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x . (Sug

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = x y z i → + x y j → + x 2 y z k → , S é formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices (

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = x y i → + 2 z j → + ( 3 y ) k → , C é a curva de inter

Se S é uma esfera e F → satisfaz as hipóteses do Teorema de Stokes, mostre que ∬ S r o tF → ⋅ d S → = 0

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → , S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção po