Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 62
Uma partícula move-se de acordo com os dados a seguir. Encontre a posição da partícula.
Passo 1
E aí, tranquilo?
Aqui o problema nos dá a função aceleração: , e nos dá duas informações, em , temos
Nesse caso, temos a aceleração e buscamos a posição .
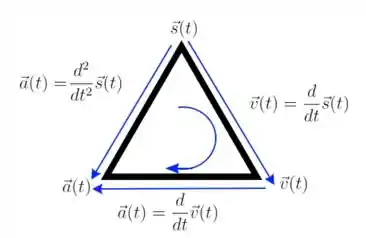
Seguindo o diagrama, a aceleração é a segunda derivada da posição.
Mas podemos seguir outro caminho, o caminho inverso aos das setas, neste caso a aceleração é a derivada da velocidade em relação ao tempo:
E por sua vez, a velocidade é a derivada da posição em relação ao tempo:
Então precisamos da antiderivada de , e aí basta encontrarmos a antiderivada novamente de para encontrarmos .
E usaremos a informação de para calcular as constantes , das duas antiderivadas que faremos.
Passo 2
Vamos calcular nossa primeira antiderivada, que nos dará a função
(E lembre-se de somar a constante) ...
Temos a relação das antiderivadas trigonométricas:
E aqui vou deixar a dica de colocar as constantes até nas antiderivadas de passagem, os professores às vezes descontam pontinhos importantes se esquecemos. (Experiência própria ☹)
Aplicando:
Usando a informação que , temos, substituindo na função:
Assim temos nossa primeira função:
Passo 3
Vamos repetir o processo para encontrar ...
Aplicando novamente as antiderivadas trigonométricas:
Usando informação de que em nossa função:
Sendo assim, a posição é dada por:
E chegamos ao fim de mais uma questão!
Entendeu tudinho? Responde aí!
