Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.3 - Ex. 26
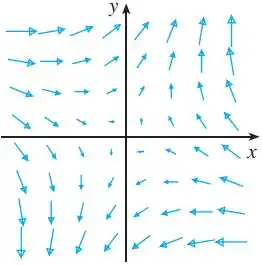
A partir do gráfico de você diria que o campo é conservativo? Explique.
Passo 1
Fala, pessoal!
Nessa questão a gente precisa avaliar se um campo vetorial é conservativo só olhando pro esboço dele.
Vamos começar lembrando que quando um campo é conservativo, temos que:
Onde é uma curva fechada.
Olhando pro esboço do gráfico, temos que avaliar os vetores que começam nos pontos de uma curva fechada.
- Caso todos estejam apontando na mesma direção ou na direção contrária da curva, é provável que a os termos de , que somam na integral, não se cancelem e o campo não seja conservativo.
- Caso estejam apontando em direções diferente (alguns na mesma direção da curva, outros na contrária), é provável que os termos se cancelem, e o campo seja conservativo.
Passo 2
Agora vamos olhar pro campo dessa questão.
Vou marcar uma curva fechada pra usar como exemplo:
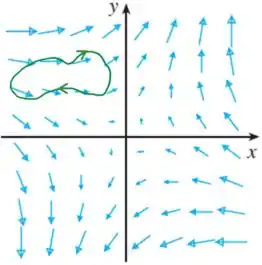
Percebe que na parte de cima da curva os vetores acompanham o sentido da curva, enquanto na parte de baixo estão no sentido oposto. Então, baseado nisso, podemos supor que o campo é realmente conservativo!
Resposta
Conservativo
Exercícios de Livros Relacionados
Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = y cos x yi + x cos x y j - sen z k
Demonstre a identidade, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se f for um campo escalar e F → e G → forem campos vetoriais, então f F → , F → ⋅ G → e F → × G → serão
Use a primeira identidade de Green para mostrar que se f for harmônica em D , e se f x , y = 0 na curva fronteira C , então ∫ ∫ D ∇ f 2 d A = 0 . (Suponha que são válidas as mesmas hipóteses do exercí
Use o Teorema de Green na forma da equação 13 para demonstrar a primeira identidade de Green: ∬ f ∇ 2 gd A = ∮ f ∇ g ⋅ n →d s - ∬ ∇ f ⋅ ∇ g d A
Demonstre a identidade, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se f for um campo escalar e F → e G → forem campos vetoriais, então f F → , F → ⋅ G → e F → × G → serão