A tabela mostra a população da Indonésia, em milhões, para a segunda metade do século XX.
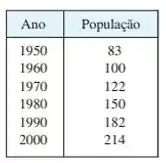
(a) Supondo que a população cresça a uma taxa proporcional tamanho, use os dados do censo de 1950 e 1960 para prever a população em 1980. Compare com o real figura.
(b) Use as figuras censitárias de 1960 e 1980 para prever a população em 2000. Compare com a população real.
(c) Use os dados do censo de 1980 e 2000 para prever a população em 2010 e comparar com a população real de 243 milhões.
(d) Use o modelo na parte (c) para prever a população em 2020. Você acha que a previsão será muito alta ou muito baixo? Por quê?
Passo 1
Oieee, bora resolver comigo:
Vamos mastigar cada parte da questão:
(a) Esta parte pede para utilizar os dados dos censos de 1950 e 1960 para prever a população da Indonésia em 1980, assumindo que o crescimento populacional ocorre a uma taxa proporcional constante ao longo do tempo. Para isso, nos podemos usar a técnica de interpolação linear, onde nós iremos calcular a taxa média de crescimento entre 1950 e 1960 e aplica essa taxa de crescimento para projetar a população em 1980. Em seguida, iremos comparar a previsão com a população real de 1980 para avaliar a precisão do modelo.
(b) Nesta parte, nós devemos usar os dados dos censos de 1960 e 1980 para prever a população em 2000. Novamente, nós podemos usar a interpolação linear para calcular a taxa média de crescimento entre 1960 e 1980 e aplicá-la para projetar a população em 2000. Iremos comparar sua previsão com a população real em 2000 para avaliar a precisão do modelo.
(c) Aqui, somos solicitados a usar os dados dos censos de 1980 e 2000 para prever a população em 2010. Utilizaremos a mesma abordagem de interpolação linear para calcular a taxa média de crescimento entre 1980 e 2000 e aplique-a para projetar a população em 2010. Iremos comparar a previsão com a população real de 243 milhões para avaliar a precisão do modelo.
(d) Finalmente, nesta parte, nós devemos usar o modelo desenvolvido na parte (c) para prever a população em 2020. Com base na tendência observada nos dados anteriores, nós devemos avaliar se sua previsão será muito alta ou muito baixa em relação à população real de 2020. Isso pode ser feito considerando fatores como mudanças nas taxas de natalidade, mortalidade e migração, bem como eventos históricos que podem influenciar o crescimento populacional.
Passo 2
Para esse problema, temos a taxa de crescimento relativa que é a taxa de crescimento dividida pela população. Chamamos a população mundial em função do tempo em horas e , sendo a taxa de crescimento relativa, temos:
Ou também,
Em que as soluções exponenciais sempre são do tipo: .
Passo 3
Tomamos 1950 como o valor inicial com uma população de 83 milhões, e após 10 anos temos uma população de 100 milhões, podemos dizer que:
Aplicando o logaritmo natural,
Tendo o valor de é só aplicar para , lembrando que
milhões
Chegou-se pouco próximo ao valor real.
Passo 4
Para a letra (b), tomamos 1960 como o valor inicial com uma população de 100 milhões, e após 20 anos temos uma população de 150 milhões, podemos dizer que:
Aplicando o logaritmo natural,
Tendo o valor de é só aplicar para , lembrando que
milhões
Ultrapassou-se o valor real.
Passo 5
Para a letra (c), tomamos 1980 como o valor inicial com uma população de 150 milhões, e após 20 anos temos uma população de 214 milhões, podemos dizer que:
Aplicando o logaritmo natural,
Tendo o valor de é só aplicar para , lembrando que
milhões
O resultado foi um pouco maior do valor real.
Passo 6
Para a letra (d), tomamos 1980 como o valor inicial com uma população de 150 milhões, e após 20 anos temos uma população de 214 milhões, podemos dizer que:
Aplicando o logaritmo natural,
Tendo o valor de é só aplicar para , lembrando que
milhões
O resultado provavelmente será um pouco maior do valor real, pois usamos os mesmos dados da letra (c).
Resposta
Vide o passo a passo.