Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.8 - Ex. 11
Uma placa quadrada com de lado está mergulhada em um líquido de peso específico . Encontre a força do fluido sobre a placa se um vértice estiver tocando a superfície e uma diagonal for perpendicular a esta.
Passo 1
Vamos compreender melhor a situação. O que ele quer dizer é que tem uma placa quadrada submersa na vertical, mas rotacionada. A gente pode encarar ela como um losango, que tem uma das diagonais paralelas à superfície.
Como temos uma região submersa na vertical, podemos usar essa relação:
Onde é o peso específico do líquido.
Vamos começar!
Passo 2
Vamos achar (largura da placa) considerando que a origem do eixo está na altura da superfície do líquido.
Vemos na figura a seguir, o nosso quadrado, de lado e de diagonais .
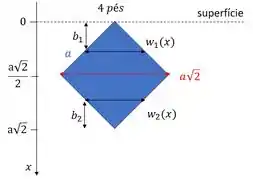
Por ela, a gente vê que nossa largura vai ser uma função definida por partes. No intervalo , podemos usar a semelhança de triângulos:
Pela figura, vemos que , logo:
No intervalo , podemos usar a semelhança de triângulos:
Pela figura, vemos que , logo:
Passo 3
Já a profundidade, vemos que é medida diretamente pelo valor de . Então, podemos escrever:
E a placa começa em e termina em .
Mas lembrando que nossa função largura é definida por partes, por isso vamos ter que calcular uma integral para cada intervalo dela e somar.
Com tudo isso, nossa força fica assim:
Passo 4
Agora é só calcular as integrais.