Do ponto , situado numa das margens de um rio, de de largura, deve-se levar energia elétrica ao ponto situado na outra margem do rio. O fio a ser utilizado na água custa o metro, e o que será utilizado fora, o metro. Como deverá ser feita a ligação para que o gasto com os fios seja o menor possível? (Suponha as margens retilíneas e paralelas.)
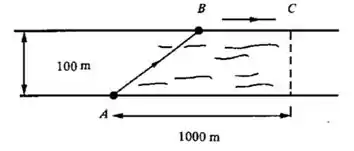
Passo 1
Peraí, vamos relembrar algumas coisas: o custo com fios dentro da água é por metro (ou seja, cada metro de até custa ) e fora da água custa o metro (cada metro de até será )
Vamos primeira definir a equação para o custo total:
Onde é a distância entre e e é a distância entre e . Vamos supor um triângulo :
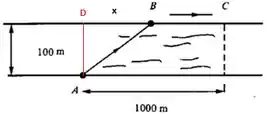
Mas precisamos encontrar relações para e né? Pra aí termos uma função com uma variável só, vamos lá!!
Passo 2
Da imagem do passo 1, temos, por relação de triângulo retângulo:
Passo 3
Também das relações de triângulo retângulo, temos
Passo 4
Última relação que precisamos encontrar pra esse exercício hehehe da figura, temos que
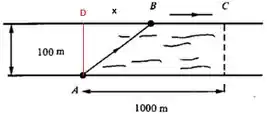
Então:
Mas e , pelo passo anterior, vale :
Passo 5
Substituindo e na equação do custo total:
Temos a função em função de certo?
Agora queremos saber quando esse custo será mínimo. Isso vai acontecer quando sua derivada for igual a 0 não é? Pois vimos que nesse ponto, a função está em seu mínimo.
Então a função admitirá um mínimo quando .
Passo 6
Vamos derivar a função e igualar a :
Derivando:
Humm, temos uma multiplicação de fatores cujo resultado dá 0
Assim,
OU:
Como , isso nuuunca vai ser !! Então nos resta usar nossa segunda opção:
Passo 7
Beleza, temos que o seno
Lembrando da relação fundamental da trigonometria:
Assim,
Passo 8
Agora vamos observar essa figura de novo:
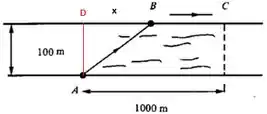
Encontramos que , então quantos metros temos em e em ?
Em podemos só fazer uma subtração né, porque
Como em temos fios fora da água, cada metro custa , então vamos gastar:
Agora vamos encontrar o comprimento usando Pitágoras:
Como está relacionado ao fio dentro da água, cada metro custará :
Ou seja, a nossa ligação será feita com de fio fora da água e dentro da água , e portanto, gastaremos , o menor valor possível para a situação.
E acabouuuuuuuu :D
Resposta
A nossa ligação será feita com de fio fora da água e dentro da água , e portanto, gastaremos , o menor valor possível para a situação.