Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 71
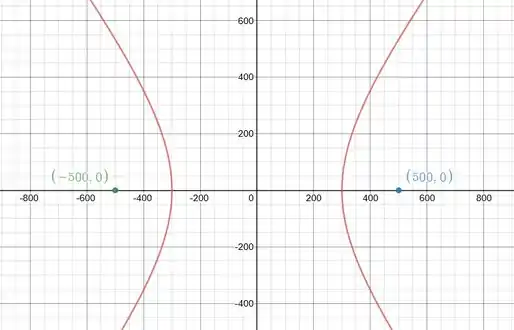
Os pontos A e B estão separados por 1000m. Pelo som de uma explosão ouvida nesses pontos em instantes diferentes, foi determinado que a localização da explosão é de 600m mais perto de A do que de B. Mostre que a localização da explosão está restrita a uma certa curva e ache uma equação dessa curva.
Passo 1
Vamos fazer essa questão bombástica!! Pela questão sabemos que a curva é uma hipérbole, porque com os 2 pontos separados 1000m, somente uma hipérbole faz com que um ponto fique mais perto de outro continuando na mesma curva, considerando que foi ouvida em instantes diferentes.
E sabemos também que a curva é feita a partir desses dois pontos, logo são o foco.
Passo 2
E para nossa formula que envolve os termos a, b e c, temos que:
Se a distância da explosão está a 600m mais perto de certo ponto do que de outro, temos que esse 600 corresponde a nossa distancia entre vértices (2a). Logo:
Portanto:
Passo 3
Temos tudo que precisamos! O formato da nossa curva e os nossos parâmetros para a equação!
Uma hipérbole tem forma:
Logo, o da nossa equação corresponde a:
