Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.21 - Ex. 21
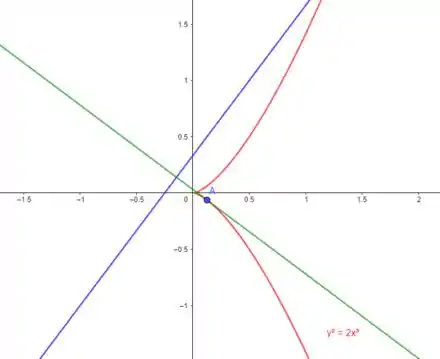
Em que pontos a reta tangente à curva é perpendicular a reta .
Passo 1
Vamos começar pela inclinação da reta tangente da curva . Vamos derivar...
E agora vamos determinar a inclinação par ser perpendicular à reta . A gente deriva...
Pra ser perpendicular, a gente faz o inverso do oposto dessa, ou seja:
Passo 2
Beleza, pra nossa reta tangente ser perpendicular à essa outra reta, precisamos que a inclinação dela seja igual a . Ou seja, precisamos descobrir os pontos em que:
Jogamos na nossa função agora...
(no ponto não temos reta tangente)
Passo 3
Show! Achamos o ponto então, é . Vamos checar isso no gráfico:
Resposta
Exercícios de Livros Relacionados
(a) Use o recurso de traçar gráficos implícitos de um CAS para esboçar o gráfico da curva C cuja equação é x 3-2 x y+y 3=0 . (b) Use o gráfico de (a) para dar um palpite sobre a coordenada x de um pon
Um estudante pergunta: “Suponha que uma derivação implícita num ponto forneça uma expressão indefinida. Isso significa que d y / d x não está definida nesse ponto?” Usando a equação x 2-2 x y+y 2 =0 c
Encontre as equações de duas retas pela origem que são tangentes à elipse de equação 2 x 2 -4 x+y 2+1=0 .
(a) Use o recurso de traçar gráficos implícitos de um CAS para esboçar o gráfico da curva C cuja equação é x 3-2 x y+y 3=0 . (b) Use o gráfico de (a) para estimar a coordenada x de um ponto do primeir
5. x 2 + y 2 = 1