Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.9 - Ex. 2

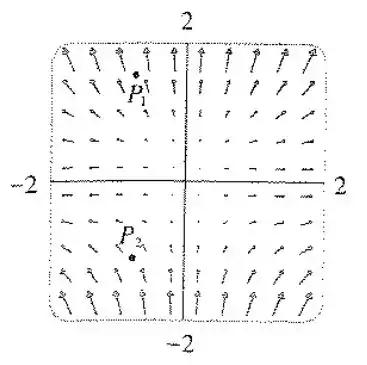
(a) Os pontos e são fontes ou sorvedouros para o campo vetorial mostrado na figura? Dê uma explicação baseada exclusivamente na figura.

(b) Dado , use a definição de divergência para verificar sua resposta da parte (a)

Passo 1

Fala, gente! 😊

Nessa questão precisamos ficar de olho na figura dada. No item (a) precisamos definir se os pontos e são fontes ou sorvedouros para o campo vetorial da figura.

Já no item (b), analisando a resposta do item (a), precisamos verificar a resposta através da definição do Teorema da Divergência quando

Passo 2

(a) Observe que os vetores que saem do ponto são maiores dos que os que entram no ponto . Logo, terá divergência positiva, sendo uma fonte.

O ponto tem as “flechas” que entram menores que as que saem, logo esse ponto tem uma divergência negativa, sendo um sorvedouro.

Passo 3

(b) Gente, a divergência de pode ser calculada como as derivadas parciais dos termos de .

Para nosso campo vetorial, temos

Logo,

Como está em uma posição onde é positivo, logo a divergência de é positiva, sendo uma fonte.

Agora está numa posição onde é negativa e supondo que

Então é negativo, sendo um sorvedouro.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema do Divergente para calcular a integral de superfície ∬ c F → ⋅ d S → , ou seja, calcule o fluxo de F → através de S . F → x , y , z = x 2 z 3 i → + 2 x y z 3 j → + x z 4 k → S é a superf

Use o Teorema do Divergente para calcular a integral de superfície ∬ c F → ⋅ d S → ; ou seja, calcule o fluxo de F → através de S . F → x , y , z = x 2 y i → + x y 2 j → + 2 x y z k → , S é a superfíc

Use o Teorema do Divergente para calcular a integral de superfície ∬ c F → ⋅ d S → ; ou seja, calcule o fluxo de F → através de S . F → x , y , z = x 3 yi - x 2 y 2j - x 2 y zk S é a superfície do sól

Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial F → na região E . F → x , y , z = x y i → + y z j → + z x k → , E é cilindro sólido x 2 + y 2 ≤ 1 , 0 ≤z ≤ 1 .

Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial F → na região E . F → x , y , z = x i → + y j → + z k → , E é a bola unitária x 2 + y 2 + z 2 ≤ 1 .