A população dos EUA no anto pode ser modelada (em milhões) pela função:
a) Com base nesse modelo, qual foi a população dos EUA em ?
b) Faça um gráfico de versus para o período de anos que vai de até .
c) Calculando um limite apropriado, mostre que o gráfico de versus tem uma assíntota horizontal com uma constante apropriada.
d) Qual é o significado da constante em b) para a previsão da população por meio desse modelo?
Passo 1
a) Para temos que a população dos EUA foi:
Só foi necessário substituir na função que nos foi dada, nada demais galera!
Passo 2
b) Se plotarmos o gráfico da função que nos foi dada teremos algo nesse tipo, galera:
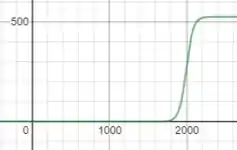
Algo importante de ressaltar é que aparenta existir uma assíntota horizontal no gráfico, não é mesmo? É um dado importante para as outras questões, vamos guardar!
Passo 3
c) Vamos ver se a função que nos foi dada possui assíntotas horizontais ou não, ok? Para fazermos isso precisamos calcular um limite específico, que é quando , então bora lá!
Aplicando o limite teremos o seguinte:
Sendo assim, fica fácil notar que há uma assíntota em , isto é, a população para de aumentar nas proximidades desse valor.
Passo 4
d) O significado matemático da assíntota é que se trata de um limite em que a curva não pode ultrapassar. Em outras palavras, quando a população dos EUA se aproximar de de habitantes haverá uma estabilidade na taxa de natalidade, isto é, a população vai parar de aumentar.
Resposta
a)
b) 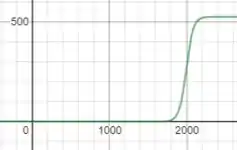
c)
d) Toda a explicação está no passo 4.