Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 34
As populações nascidas em ambientes fechados crescem devagar no início, quando há relativamente poucos membros, e depois mais rapidamente, à medida que o número de membros reprodutores aumenta e os recursos permanecem abundantes, e, por fim, tornam a crescer a um ritmo lento, conforme a população atinge a capacidade de sustentação daquele ambiente.
- represente graficamente a derivada da população de moscas-da-fruta. O gráfico da população é reproduzido aqui.
- Durante quais dias a população parece estar crescendo mais rapidamente? E mais devagar?
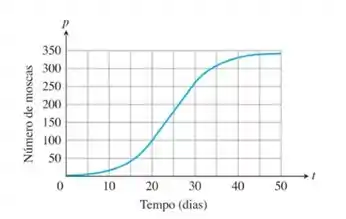
Passo 1
Resolvendo o item (a)
Para esboçar o graficamente a derivada devemos usar os coeficientes angulares da reta tangente a intervalos frequentes, registrando os pares e unindo eles com uma curva suave.
Passo 2
No gráfico apresentado na questão, podemos usar intervalos correspondente a 10 dias.
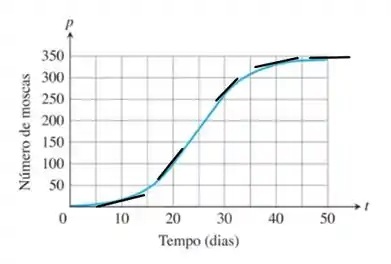
Observando as retas tangentes, podemos calcular o coeficiente angular de cada uma delas.
Passo 3
Trançando os pontos com uma curva suave, temos:
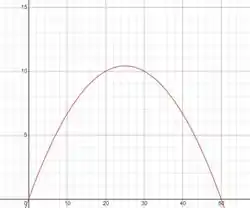
Passo 4
Resolvendo o item (b)
Podemos ver que a população cresce mais nos pontos onde o gráfico de está mais inclinado, ou seja, nos pontos onde a derivada é maior. Por isso, podemos afirmar que a população cresce mais entre os dias 20 e 30.
Já sobre os dias com menor crescimento, podemos afirmar que são os dias até o 10º dia e os dias de 40 a 50.
Resposta
Ei, a resposta está no passo a passo :)