Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 50
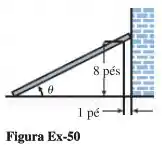
Uma prancha é usada para escorar um muro e deve passar por cima de uma cerca de de altura e a do muro (Figura Ex-50). Qual é o comprimento da menor escora que pode ser usada? [Sugestão: Expresse o comprimento da escora em termos do ângulo mostrado na figura].
Passo 1
Então pessoal, antes de começarmos com os cálculos de fato devemos prestar atenção em uma coisinha na figura. Vamos chamar o tamanho da escora de , ok? Pela figura temos um comprimento que vai até de distância do muro e um outro comprimentozinho que é o restante até chegar ao muro. Em outras palavras, temos:
Show! A sugestão do enunciado é que expressemos o comprimento que acabamos de escrever em termos de , então vamos fazer isso!
Passo 2
Para o triângulo formado com , temos:
E para o triângulo formado com , temos:
Substituindo na expressão de , teremos:
Ok, expressamos em função do ângulo da escora.
Passo 3
Como estamos interessados em saber o comprimento da menor escora que pode ser usada, então estamos falando de ponto de mínimo, certo? Utilizando as noções de cálculo, teremos:
Em termos de seno e cosseno:
Igualando nossa derivada a zero:
Isso só será zero se:
Ok, encontramos nosso ângulo de minimização!
Passo 4
Desse valor de mínimo que encontramos tiramos que:
Sendo assim, o comprimento da menor escora será:
E esse é o nosso resultado! 😉