Os problemas 8 a 13 envolvem equações da forma . Em cada problema, esboce o gráfico de em função de , determine os pontos críticos (de equilíbrio) e classifique-os como assintoticamente estável, instável ou semiestável (Veja o Problema 7). Desenhe a reta de fase e esboce diversos gráficos de soluções no plano .

Olhando para nossa função dada, temos que

Implica que, nossa função só será zero se e somente se

ou

O que nos dá e

O gráfico de é dado por

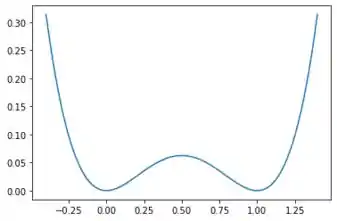
Olhando para nosso gráfico, vemos que, do lado esquerdo de cada um nos nosso pontos, temos uma reta descrecente e do lado diretos, uma reta crescente. Assim temos que, de uma lado da nosso solução, as soluções se aproximam da nossa solução, enquando do lado direito as soluções se afastam da nosso solução. Assim temos ques os dois pontos são ditos semi-estáveis