8. Uma pessoa jovem sem capital inicial investe k reais por ano a uma taxa anual de retorno r. Suponha que os investimentos são feitos continuamente e que o retorno é capitalizadocontinuamente.(a) Determine a quantia S(t) acumulada em qualquer instante t.(b) Se r = 7,5%, determine k de modo que 1 milhão de reais esteja disponível para a aposentadoria em 40 anos.(c) Se k = R$ 2.000,00 por ano, determine qual deve ser a taxa de retorno r para se ter 1milhão de reais em 40 anos.

c. Descobrimos no item a) que a equação que rege os juros compostos com aportes constantes é

Agora vamos usar os dados de contorno

Agora podemos descobrir qual é o rendimento anual.

E infelizmente não temos solução analítica para essa equação, podemos resolver por um argumento geométrico. Manipulando essa equação temos

A solução será o ponto onde as curvas 500r e se cruzam.

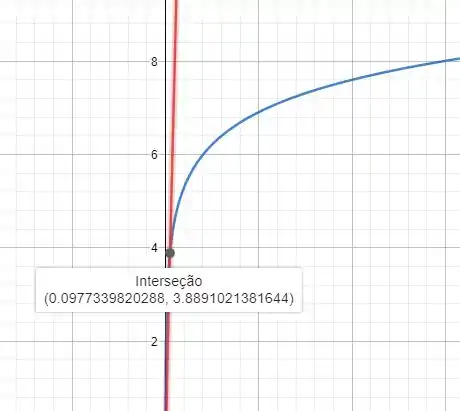
Logo nosso rendimento é

Na vida real para descobrirmos quanto precisamos para construir patrimônio, precisamos levar em conta a inflação que destrói nosso poder de compra. Um jeito pratico é fazer o seguinte

Onde o Rendimento real tem que ser a inflação mais esse r que calculamos com essa equação diferencial. Terminamos por aqui. Te vejo na próxima resolução

: )