Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 25
Encontre uma raiz da equação:
aplicando o método de Newton para polinômios.
Passo 1
Faala ae, beleza?? Sendo bem sincero, essa questão tem um problema: não existe valores negativos de , então, a gente não conseguiria achar um intervalo em que tem uma raiz e nem um chute inicial... A única forma é, de fato plotando a função.
Então, vamos plotar essa função para termos um chute inicial:
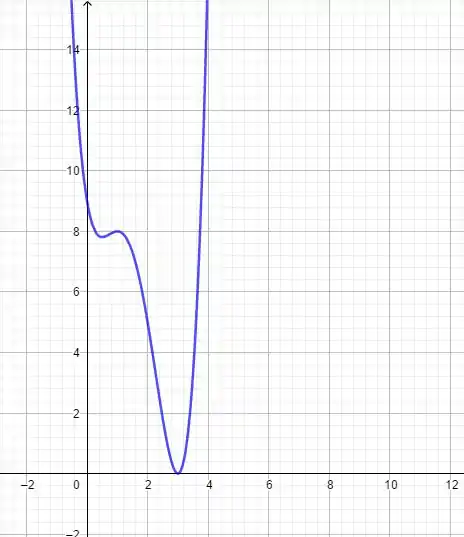
Conseguimos ver que a raiz está entre e , certo? No caso, nosso chute seria , intuitivamente, certo? Mas repare que essa já é a raiz:
Com isso, a gente já acharia o valor da raiz... Sem método algum, mas com certeza não é o intuito desse problema. Então, vamos adaptá-lo, beleza? Vamos fingir que nosso chute inicial é e vamos aplicar o método de Newton. 😊 Como o problema também não dá o critério de parada kkkk vamos admitir .
O intuito será só aplicar o método para dar uma treinada...
Passo 2
Primeiro a gente tem:
Derivando, vamos ter:
Aplicando na fórmula de Newton, teremos:
Se fizermos
Conseguimos chegar em:
Vamos usar 4 casas decimais! O critério de parada:
Com isso, podemos dizer que nosso resultado é ... A ideia é dar , como sabemos. Mas o problema foi mal formulado... Então, não temos como saber exatamente como o autor queria que resolvêssemos, só sabemos que tínhamos que usar o método de Newton rs.