Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.4 - Ex. 42

Use integração para obter π r 2 unidades de área para a área da região cercada por uma circunferência com r unidades de raio.

Passo 1

Pessoal, o primeiro passo é identificar que área é essa, né? Vamos desenhar uma circunferência de raio r e centro na origem. Lembre-se que, nesse caso, a equação vai ser x 2 + y 2 = r 2 e o gráfico será:

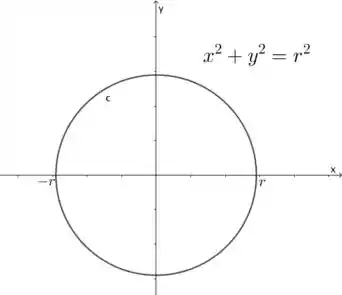
Se queremos calcular a área da região cercada pela circunferência, podemos calcular a área da semicircunferência e multiplicar por 2, ou, ainda, calcular a área de um quarto de circunferência e multiplicar por 4, para isso vamos precisar da função da semicircunferência. Basta isolar o y na equação do círculo.

Dessa forma, temos y 2 = r 2 - x 2   →         y = r 2 - x 2   , essa é a equação da semicircunferência acima do eixo x , basta integrar essa função no intervalo [ 0 , r ] e vamos obter um quarto da área procurada. Sendo assim, a área da região pedida será dada por:

A = 4 ∫ 0 r r 2 - x 2 d x

Passo 2

Podemos resolver essa integral de duas formas: calcular a indefinida e no final resolver a definida ou ir resolvendo direto trocando os limites de integração.

Nesta questão, nós vamos resolver a definida, no caminho, trocando os limites de integração, ok? Agora, para resolver, vamos precisar saber qual substituição trigonométrica usar.

Como nós temos a expressão r 2 - x 2 , isso indica a substituição com o seno, como vocês podem ver a seguir no quadro de substituições com os respectivos triângulos e intervalos.

Olhando o quadrinho, percebemos que a substituição deve ser x = r sen ⁡ θ .

Passo 3

Façamos então a substituição:

x = r sen ⁡ θ d x = r cos θ ⁡ d θ      

Dessa forma, - ( x ) 2 = - r 2 sen 2 ⁡ θ     →     r 2 - x 2 = r 2 - r 2 sen 2 ⁡ θ = r 2 ( 1 - sen 2 ⁡ θ ) = r 2 cos 2 ⁡ θ .

Agora vamos trocar a variável da integral, mas, antes vamos obter os limites de integração na variável θ . Seja então:

x = 0 → 0 = r sen ⁡ θ →       θ = 0 x = r → r = r sen ⁡ θ →         θ = π 2

Passo 4

Substituindo tudo na integral e desenvolvendo, temos:

A = 4 ∫ 0 r r 2 - x 2 d x = 4 ∫ 0 π 2 r 2 cos 2 ⁡ θ r c o s   θ d θ = 4 ∫ 0 π 2 r 2 cos 2 ⁡ θ d θ =

= 4 r 2 ∫ 0 π 2 cos 2  θ ⁡ d θ

Passo 5

Agora, para resolver essa integral, vamos utilizar a relação cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 . Sendo assim,

A = 4 r 2 ∫ 0 π 2 1 + cos ⁡ 2 θ 2 ⁡ d θ = 2 r 2 ∫ 0 π 2 1 + cos ⁡ 2 θ ⁡ d θ

Sabemos da integral definida que:

∫ a b f x d x = F b - F a

Em que F é uma primitiva de f .

A = 2 r 2 ∫ 0 π 2 1 + cos ⁡ 2 θ ⁡ d θ = 2 r 2 θ + sen ⁡ 2 θ 2 0 π 2

A = 2 r 2 π 2 + sen ⁡ 2 ⋅ π 2 2 - 0 + sen ⁡ 2 0 2

A = 2 r 2 π 2 + sen ⁡ π 2 = 2 r 2 π 2 = π r 2   u . a

Está mostrado o resultado.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o centroide da região limitada pelo laço da curva y 2 = x 2 - x 3 .
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (12) A parábola y = 2 x + 1 , x + y = 7 e x = 8 .
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (13) A parábola y = x 2 - 4 e y = 2 x - x ² ².
Ache o centro de massa de três partículas de igual amssa localizadas em 4 , - 2 ,- 3,0 e( 1 ,5 ) .
Prove que o centro de massa de três partículas com igual massa num plano está no ponto de intersecção das medianas do triângulo cujos vértices são os pontos onde estão as partículas.