Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 34

34) Prove que não existe reta tangente à hipérbole x ² - y 2 = 1 que passe pela origem.

Passo 1

Sabendo que a equação da hipérbole é x ² - y 2 = 1 , nós concluímos que o centro da hipérbole se encontra na origem (0,0).

Se fizermos y = 0 :

x 2 - 0 = 1

x = ± 1

Desenhando:

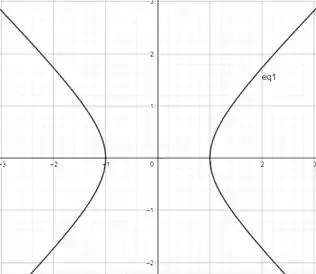
Para que uma reta cruze a origem sua equação deve ser do tipo

y = m x

Substituindo na equação da hipérbole:

x ² - ( m x ) 2 = 1

x 2 1 - m 2 - 1 = 0

Para que haja uma reta tangente o discriminante dessa equação quadrática deve ser igual a 0, indicando que há pelo menos um ponto onde a reta toca a hipérbole:

∆ = b 2 - 4 a c

∆ = 0 2 - 4 1 - m 2 - 1 = 4 - m ²

4 - m 2 = 0  

m = ± 2

Para estes valores de m podemos avaliar x:

m = ± 2 → x = 1 1 - m 2 = 1 1 - 4 = - 1 3

Ou seja, não há valor real para x. Isso indica que a reta que passa pela origem não toca a hipérbole em nenhum valor real.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico 2 y 2 - 4 x 2 = 1
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Centro C ( 5,1 ) , um foco em ( 9,1 ) , eixo imaginário mede 4 2 .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Focos em ( 3,4 ) e F ( 3 , - 2 ) , excentricidade e = 2 .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Centro C ( 0,0 ) , eixo real sobre O y , b = 8 e excentricidade e = 5 3 .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Vértices A 1 ( - 3 , - 4 ) e A 2 ( - 3,4 ) , hipérbole equilátera.