Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 33
Prove que os pontos , , e são vértices de um paralelogramo.
Passo 1
Precisamos lembrar que o que define um paralelogramo é que seus lados opostos são paralelos. Para provar que são, vamos usar o conceito de inclinação de reta.
Passo 2
Vamos primeiro marcar os pontos num gráfico para facilitar a visualização.
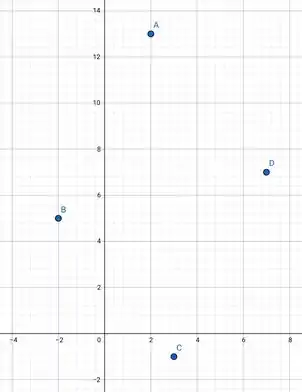
Passo 3
Agora, encontramos as retas-suporte de cada lado:
Para o lado , .
Para o lado , .
Para o lado , .
Para o lado , .
Como as inclinações dos lados opostos são iguais, temos que os pontos são vértices de um paralelogramo.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule a excentricidade de uma hipérbole, sabendo que as extremidades das cordas que contêm algum foco e são perpendiculares à reta focal são vértices de um quadrado.
Dados os pontos distintos M e N e o número k , prove que, se k1 , o lugar geométrico dos pontos X cuja projeção ortogonal Q sobre a reta M N pertence ao segmento M N e satisfaz a relação X Q → 2 = k 2
Dada a elipse E de parâmetros geométricos a , b , c , e eixo maior A 1 A 2 sejam P um ponto e Q sua projeção ortogonal sobre a reta focal. Mostre que, se P pertence à elipse, então Q pertence ao segme
Calcule a área do losango cujos vértices são os focos e as extremidades do eixo menor da elipse de equação x 2 / a 2 + y 2 / b 2 = 1 . Em que condições esse losango é um quadrado?
Seja P um ponto da elipse E : x 2 / a 2 + y 2 / b 2 = 1 . Suponha que P ≠ B 1 e P ≠ B 2 e considere os pontos R e S de intersecção de O x com as retas B 1 P e B 2 P . Prove que O R → ⋅ O S → = a 2 . S